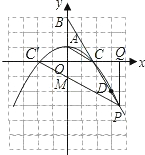
解:(1)∵A(0,1),B(0,3),
∴AB=2,
∵△ABC是等腰三角形,且点C在x轴的正半轴上,
∴AC=AB=2,
∴OC=
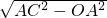
=

.
∴C(

,0).
设直线BC的解析式为y=kx+3,
∴

k+3=0,
∴k=-

.
∴直线BC的解析式为y=-

x+3.
(2)∵抛物线y=ax
2+bx+c关于y轴对称,
∴b=0.
又抛物线y=ax
2+bx+c经过A(0,1),D(3,-2)两点.
∴
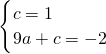
解得
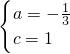
∴抛物线的解析式是y=-

x
2+1.
在Rt△AOC中,OA=1,AC=2,易得∠ACO=30°.
在Rt△BOC中,OB=3,OC=

,易得∠BCO=60°.
∴CA是∠BCO的角平分线.
∴直线BC与x轴关于直线AC对称.
点P关于直线AC的对称点在x轴上,则符合条件的点P就是直线BC与抛物线y=-

x
2+1的交点.
∵点P在直线BC:y=-

x+3上,故设点P的坐标是(x,-

x+3).
又∵点P(x,-

x+3)在抛物线y=-

x
2+1上,
∴-

x+3=-

x
2+1.
解得x
1=

,x
2=2

.
故所求的点P的坐标是P
1(

,0),P
2(2

,-3).
(3)要求PM+CM的取值范围,可先求PM+C′M的最小值.
(I)当点P的坐标是OC=

时,点P与点C重合,
故PM+CM=2CM.
显然CM的最小值就是点C到y轴的距离为

,
∵点M是y轴上的动点,
∴PM+CM无最大值,
∴PM+CM≥2

.
(II)当点P的坐标是(2

,-3)时,由点C关于y轴的对称点C′(-

,0),
故只要求PM+MC'的最小值,显然线段PC'最短.易求得PC'=6.
∴PM+CM的最小值是6.
同理PM+CM没有最大值,
∴PM+CM的取值范围是PM+CM≥6.
综上所述,当点P的坐标是(

,0)时,PM+CM≥2

,
当点P的坐标是(2

,-3)时,PM+CM≥6.
分析:(1)根据第三个顶点C在x轴的正半轴上,利用勾股定理求出OC的长,进而求出C点坐标,应用待定系数法即可求出直线BC的解析式;
(2)由于抛物线解析式关于y轴对称,可知一次项系数为0,利用待定系数法,设出一般式,将A(0,1),D(3,-2)代入解析式即可求出二次函数解析式;根据轴对称定义和角平分线的定义,利用特殊角判断出则符合条件的点P就是直线BC与抛物线y=-

x
2+1的交点.
(3)根据轴对称定义和性质,作出C关于y轴的对称点C′,将求PM+CM的取值范围转化为求PM+C′M的取值范围.
点评:此题考查了对函数题综合应用和分析解答的能力.(1)(2)小题难度不大,主要应用待定系数法即可解答,(3)要根据轴对称的性质,将折线转化为两点之间线段最短的问题来解答.

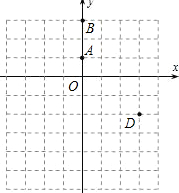 半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.
半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上. 解:(1)∵A(0,1),B(0,3),
解:(1)∵A(0,1),B(0,3),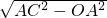 =
= .
. ,0).
,0). k+3=0,
k+3=0, .
. x+3.
x+3.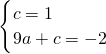
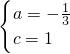
 x2+1.
x2+1. ,易得∠BCO=60°.
,易得∠BCO=60°. x2+1的交点.
x2+1的交点. x+3上,故设点P的坐标是(x,-
x+3上,故设点P的坐标是(x,- x+3).
x+3). x+3)在抛物线y=-
x+3)在抛物线y=- x2+1上,
x2+1上, x+3=-
x+3=- x2+1.
x2+1. ,x2=2
,x2=2 .
. ,0),P2(2
,0),P2(2 ,-3).
,-3). 时,点P与点C重合,
时,点P与点C重合, ,
, .
. ,-3)时,由点C关于y轴的对称点C′(-
,-3)时,由点C关于y轴的对称点C′(- ,0),
,0), ,0)时,PM+CM≥2
,0)时,PM+CM≥2 ,
, ,-3)时,PM+CM≥6.
,-3)时,PM+CM≥6. x2+1的交点.
x2+1的交点.
