
【题目】如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是_____.

【答案】①②③④⑤.
【解析】先计算出DE=2,EC=4,再根据折叠的性质AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,然后根据“HL”可证明Rt△ABG≌Rt△AFG,则GB=GF,∠BAG=∠FAG,所以∠GAE=![]() ∠BAD=45°;GE=GF+EF=BG+DE;设BG=x,则GF=x,CG=BC﹣BG=6﹣x,在Rt△CGE中,根据勾股定理得(6﹣x)2+42=(x+2)2,解得x=3,则BG=CG=3,则点G为BC的中点;同时得到GF=GC,根据等腰三角形的性质得∠GFC=∠GCF,再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF,然后根据三角形外角性质得∠BGF=∠GFC+∠GCF,易得∠AGB=∠GCF,根据平行线的判定方法得到CF∥AG;过F作FH⊥DC,则△EFH∽△EGC,△EFH∽△EGC,由相似比为
∠BAD=45°;GE=GF+EF=BG+DE;设BG=x,则GF=x,CG=BC﹣BG=6﹣x,在Rt△CGE中,根据勾股定理得(6﹣x)2+42=(x+2)2,解得x=3,则BG=CG=3,则点G为BC的中点;同时得到GF=GC,根据等腰三角形的性质得∠GFC=∠GCF,再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF,然后根据三角形外角性质得∠BGF=∠GFC+∠GCF,易得∠AGB=∠GCF,根据平行线的判定方法得到CF∥AG;过F作FH⊥DC,则△EFH∽△EGC,△EFH∽△EGC,由相似比为![]() ,可计算S△FGC.根据同底等高的三角形的面积相等即可得到结论.
,可计算S△FGC.根据同底等高的三角形的面积相等即可得到结论.
解:∵正方形ABCD的边长为6,CE=2DE,
∴DE=2,EC=4,
∵把△ADE沿AE折叠使△ADE落在△AFE的位置,
∴AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,
在Rt△ABG和Rt△AFG中,AB=AE,AG=AG,
∴Rt△ABG≌Rt△AFG(HL),
∴GB=GF,∠BAG=∠FAG,
∴∠GAE=∠FAE+∠FAG=![]() ∠BAD=45°,所以①正确;
∠BAD=45°,所以①正确;
设BG=x,则GF=x,C=BC﹣BG=6﹣x,
在Rt△CGE中,GE=x+2,EC=4,CG=6﹣x,
∵CG2+CE2=GE2,
∴(6﹣x)2+42=(x+2)2,解得x=3,
∴BG=3,CG=6﹣3=3
∴BG=CG,所以②正确;
∵EF=ED,GB=GF,
∴GE=GF+EF=BG+DE,所以③正确;
∵GF=GC,
∴∠GFC=∠GCF,
又∵Rt△ABG≌Rt△AFG,
∴∠AGB=∠AGF,
而∠BGF=∠GFC+∠GCF,
∴∠AGB+∠AGF=∠GFC+∠GCF,
∴∠AGB=∠GCF,
∴CF∥AG,所以④正确;
过F作FH⊥DC
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴![]() =
=![]() ,
,
EF=DE=2,GF=3,
∴EG=5,
∴△EFH∽△EGC,
∴相似比为: ![]() =
=![]() ,
,
∴S△FGC=S△GCE﹣S△FEC=![]() ×3×4﹣
×3×4﹣![]() ×4×(
×4×(![]() ×3)=
×3)=![]() =3.6,
=3.6,
连接AC,
∵CF∥AG,
∴S△FCA=S△FGC=3.6,
所以⑤正确.
故正确的有①②③④⑤,
故答案为:①②③④⑤.

“点睛”本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了三角形全等的判定与性质,勾股定理和正方形的性质.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE= ![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE. 
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间平均距离,即1.4960亿千米,用科学记数法表示1个天文单位应是( )
A.1.4960×107千米
B.14.960×107千米
C.1.4960×108千米
D.0.14960×109千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】支付宝与“滴滴打车”联合推出优惠,“滴滴打车”一夜之间红遍大江南北,据统计,2016年“滴滴打车”账户流水总金额达到4730000000元,用科学记数法表示为( )
A.4.73×108
B.4.73×109
C.4.73×1010
D.4.73×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策,这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措.二孩政策出台后,某家庭积极响应政府号召,准备生育两个小孩(生男生女机会均等,且与顺序有关).
(1)该家庭生育两胎,假设每胎都生育一个小孩,求这两个小孩恰好是1男1女的概率;
(2)该家庭生育两胎,假设第一胎生育一个小孩,且第二胎生育一对双胞胎,求这三个小孩中至少有1个女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( ) 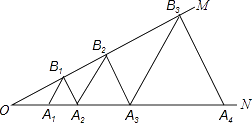
A.6
B.12
C.32
D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程(m﹣3)x2+2mx+m+1=0有两个不相等的实数根,并且这两个根又不互为相反数.
(1)求m的取值范围;
(2)当m在取值范围内取最小正偶数时,求方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com