
 已知y关于x的二次函数y=x2+2mx-3m2(m≠0)的图象的顶点为A,与x轴交于点B,C,与y轴交于点D.
已知y关于x的二次函数y=x2+2mx-3m2(m≠0)的图象的顶点为A,与x轴交于点B,C,与y轴交于点D.分析 (1)将m=1代入可得到抛物线的解析式,然后利用配方法求得点A的坐标,将x=0代入可求得点D的纵坐标;
(2)分为∠ABN=90°,∠BAN=90°,∠ANB=90°三种情况求解即可;
(3)先利用配方法求得点A的坐标,然后令y=0可求得点B、C的坐标,然后利用等边三角形的性质求解即可.
解答 解:(1)当m=1,y=x2+2x-3,
当x=0时,y=-3.
∴D(0,-3).
∵y=x2+2x-3=(x+1)2-4,
∴A(-1,-4).
故答案为:(-1,-4);(0,-3).
(2)如图所示: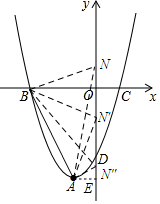
令x2+2x-3=0,解得:x=-3或x=1,
∴B(-3,0).
设直线AB的解析式为y=kx+b,将点A和点B的坐标代入得:$\left\{\begin{array}{l}{-3k+b=0}\\{-k+b=-4}\end{array}\right.$,
解得:k=-2,b=-6.
∴直线AB的解析式为y=-2x-6.
①当∠ABN=90°.设直线BN的解析式为y=$\frac{1}{2}$x+c,将点B的坐标代入得:-3×$\frac{1}{2}$+c=0,解得:c=$\frac{3}{2}$.
∴点N的坐标为(0,$\frac{3}{2}$).
②当∠BAN″=90°时,设直线BN″的解析式为y=$\frac{1}{2}$x+d,将点A的坐标代入得:-1×$\frac{1}{2}$+d=-4,解得:d=-$\frac{7}{2}$.
∴点N″的坐标为(0,-$\frac{7}{2}$).
③∠BN′A=90°时,过点A作AE⊥y轴,则OB=3,OE=4,AE=1.
∵∠BN′O+∠N′BO=90°,∠AN′E+∠BN′O=90°,
∴∠N′BO=∠AN′E.
又∵∠BON′=∠AEN′=90°,
∴△BON′∽△N′EA.
∴$\frac{ON′}{AE}=\frac{OB}{N′E}$.
设ON′=x,则N′E=4-x.则$\frac{x}{1}=\frac{3}{4-x}$,解得:x=1或x=3.
所以ON′=1或ON′=3.
∴点N′为(0,-1)或(0,-3).
综上所述,点N的坐标为(0,$\frac{3}{2}$)或(0,-1)或(0,-3)或(0,-$\frac{7}{2}$).
(3)y=x2+2mx-3m2=(x+m)2-4m2=(x+3m)(x-m)
∴抛物线与两坐标轴的交点坐标为(-3m,0)和(m,0),点A的坐标为(-m,-4m2).
∵△ABC为等边三角形,
∴$\frac{4{m}^{2}}{|2m|}$=$\sqrt{3}$.
当m>0时,2m=$\sqrt{3}$,解得m=$\frac{\sqrt{3}}{2}$,
当m<0时,-2m=$\sqrt{3}$,解得m=-$\frac{\sqrt{3}}{2}$.
综上所述,当m=±$\frac{\sqrt{3}}{2}$时,△ABC为等边三角形.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数的解析式,相似三角形的性质和判定、等边三角形的性质,熟练掌握相关知识是解题的关键.


科目:初中数学 来源: 题型:填空题
 在期中测试中,我们计算过三边分别为AB=8,BC=5,AC=7的△ABC的内切圆的半径,如图,⊙O是△ABC的外接圆.AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.
在期中测试中,我们计算过三边分别为AB=8,BC=5,AC=7的△ABC的内切圆的半径,如图,⊙O是△ABC的外接圆.AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
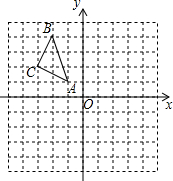 如图,A(-1,1),B(-2,4),C(-3,2).
如图,A(-1,1),B(-2,4),C(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列各式: 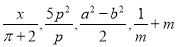 ,其中分式共有( ).
,其中分式共有( ).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:解答题
如图,点B、E、C、F在同一直线上,AC与DE相交于点G,∠A=∠D,AC∥DF,求证:AB∥DE.
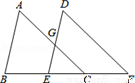
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列计算中,结果是 的是( )
的是( )
A. a2+a4 B. a2·a3 C. a12÷a2 D. (a2)3
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省佛山市顺德区八年级3月月考数学试卷(解析版) 题型:填空题
如图,OP平分∠AOB,PC⊥OB于点C,且PC=3,点P到OA的距离为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com