
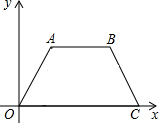
 如图,在直角坐标平面内,四边形OABC是等腰梯形,其中OA=AB=BC=4,tan∠BCO=
如图,在直角坐标平面内,四边形OABC是等腰梯形,其中OA=AB=BC=4,tan∠BCO=| 3 |
| 3 |
| 3 |
| 3 |
|
|
| ||
| 6 |
4
| ||
| 3 |
 (2)有两种情况,
(2)有两种情况,| 3 |
4
| ||
| 3 |
| 3 |
| 3 |

4
| ||
| 3 |
| 7 |
4
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 3 |
| 3 |
| 3 |
| PM2+QM2 |
| 7 |
| 7 |
| 7 |
4
| ||
| 3 |
4
| ||
| 3 |
| 7 |
| 7 |


科目:初中数学 来源: 题型:
 如图,小颖利用有一个锐角是45°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5米,小颖的眼睛距地面的距离AB为1.5米,求这棵树的高度.
如图,小颖利用有一个锐角是45°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5米,小颖的眼睛距地面的距离AB为1.5米,求这棵树的高度.查看答案和解析>>
科目:初中数学 来源: 题型:
| 10 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:

| 5 |
| GC |
| EC |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
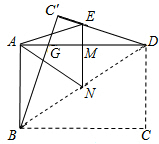 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com