解:(1)∵AB=AC,
∴∠B=∠C,
∵DE∥AB,
∴∠B=∠CED,∠AFD=∠FDE=90°,
∴∠C=∠CED,
∴DC=DE.
在Rt△ADF中,∵∠A=45°,
∴∠ADF=45°=∠A,
∴AF=DF=x,
∴
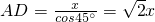
,
∴

,
∴y=

(DE+FB)×DF=

(1-

x+1-x)x=-

(

+1)x
2+x.
∵点D保持在AC上,且D不与A重合,
∴0<AD≤1,
∴0<

x≤1,
∴0<x≤

.
故y=-

(

+1)x
2+x,自变量x的取值范围是0<x≤

;
(2)∵y=-

(

+1)x
2+x,
∴当
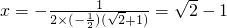
<

时,y有最大值;
(3)∵y=-

(

+1)x
2+x,0<x≤

,-

<0,
∴当
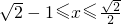
时,y随x的增大而减小.
分析:(1)当点D保持在AC上时,正方形与△ABC重叠部分为直角梯形DEBF,根据直角梯形的面积公式,只需用含x的代数式分别表示出上底DE、下底BF及高DF的长度即可.由△ADF为等腰直角三角形,可得高DF=AF=x;则AD=

x,下底BF=AB-AF=1-x;进而得出CD=AC-AD=1-

x,再根据等腰三角形及平行线的性质可证∠C=∠CED,得出上底DE=CD1-

x;根据点D保持在AC上,且D不与A重合,可知0<AD≤1,从而求出自变量x的取值范围;
(2)由(1)知,y是x的二次函数,根据二次函数的性质,可知当x=-

时,y的值最大;
(3)根据二次函数的增减性,当a<0时,在对称轴x=-

的右侧,y的值随x的增大而减小.
点评:本题考查了正方形、平行线的性质,等腰三角形的性质与判定,直角梯形的面积及二次函数的性质,综合性较强,难度中等.

 别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.
别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.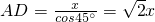 ,
, ,
, (DE+FB)×DF=
(DE+FB)×DF= (1-
(1- x+1-x)x=-
x+1-x)x=- (
( +1)x2+x.
+1)x2+x. x≤1,
x≤1, .
. (
( +1)x2+x,自变量x的取值范围是0<x≤
+1)x2+x,自变量x的取值范围是0<x≤ ;
; (
( +1)x2+x,
+1)x2+x,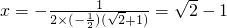 <
< 时,y有最大值;
时,y有最大值; (
( +1)x2+x,0<x≤
+1)x2+x,0<x≤ ,-
,- <0,
<0,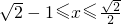 时,y随x的增大而减小.
时,y随x的增大而减小. x,下底BF=AB-AF=1-x;进而得出CD=AC-AD=1-
x,下底BF=AB-AF=1-x;进而得出CD=AC-AD=1- x,再根据等腰三角形及平行线的性质可证∠C=∠CED,得出上底DE=CD1-
x,再根据等腰三角形及平行线的性质可证∠C=∠CED,得出上底DE=CD1- x;根据点D保持在AC上,且D不与A重合,可知0<AD≤1,从而求出自变量x的取值范围;
x;根据点D保持在AC上,且D不与A重合,可知0<AD≤1,从而求出自变量x的取值范围; 时,y的值最大;
时,y的值最大; 的右侧,y的值随x的增大而减小.
的右侧,y的值随x的增大而减小.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为