
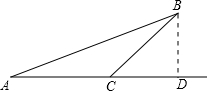
 解:设BD=x,由题意可知:∠BAD=30°,∠BCD=45°,AC=20×2=40千米,
解:设BD=x,由题意可知:∠BAD=30°,∠BCD=45°,AC=20×2=40千米,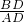 =
=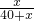 =
= ,
, ≈54.6,
≈54.6,

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
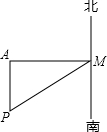 如图,在港口M的南偏西60方向有一座小岛P,一船以每小时20千米的速度从港口M出发,沿正西方向行驶,半个小时后,这艘船在A处测得小岛在船的正南方向,那么小岛P与港口M相距
如图,在港口M的南偏西60方向有一座小岛P,一船以每小时20千米的速度从港口M出发,沿正西方向行驶,半个小时后,这艘船在A处测得小岛在船的正南方向,那么小岛P与港口M相距查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:013
![]()

查看答案和解析>>
科目:初中数学 来源:2012年人教版初中数学九年级下28.2解直角三角形练习卷(解析版) 题型:选择题
如图:一只船以每小时20千米的速度向正东航行,起初船在A处看见一灯塔B在船的北偏东60°,2小时后,船在C处看见这个灯塔在船的北偏东45°,则灯塔B到船的航海线AC的距离是 [ ]千米.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com