练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某公司有甲种原料260kg，乙种原料270kg，计划用这两种原料生产A、B两种产品共40件．生产每件A种产品需甲种原料8kg，乙种原料5kg，可获利润900元；生产每件B种产品需甲种原料4kg，乙种原料9kg，可获利润1100元．设安排生产A种产品x件．
    （1）完成下表

     
    		甲（kg）
    		乙（kg）
    		件数（件）
    A
    		 
    		5x
    		x
    B
    		4（40-x）
    		 
    		40-x
    （2）安排生产A、B两种产品的件数有几种方案？试说明理由；
    （3）设生产这批40件产品共可获利润y元，将y表示为x的函数，并求出最大利润．

    （1）见解析
    （2）共有三种方案：
    方案一：A产品23件，B产品17件，
    方案二：A产品24件，B产品16件，
    方案三：A产品25件，B产品15件；
    （3）y=-200x+44000   39400元

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    已知：甲、乙两车分别从相距300千米的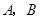两地同时出发相向而行，其中甲到地后立即返回，下图是它们离各自出发地的距离（千米）与行驶时间（小时）之间的函数图象．
    （1）求甲车离出发地的距离（千米）与行驶时间（小时）之间的函数关系式，并写出自变量的取值范围；
    （2）当它们行驶到与各自出发地的距离相等时，用了小时，求乙车离出发地的距离（千米）与行驶时间（小时）之间的函数关系式；
    （3）在（2）的条件下，求它们在行驶的过程中相遇的时间．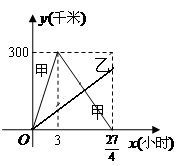

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，一次函数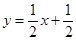的图象与x轴交于点A，与y轴交于点B，与反比例函数的图象在第一象限内交于点C，CD⊥x轴于点D，OD＝2AO，求反比例函数的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图,是一张放在平面直角坐标系中的矩形纸片,为原点,点在轴的正半轴上,,在上取一点,将纸片沿翻折,使点落在边上的点处,求直线的解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，二次函数y=(x-2)2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点，已知一次函数y=kx+b的图象上的点A（1,0）及B.

    （1）求二次函数与一次函数的解析式；
    （2）根据图象，写出满足kx+b（x-2）2+m的x的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售， 售出土豆千克数与他手中持有的钱(含备用零钱)的关系如图所示，结合图象回答下列问题：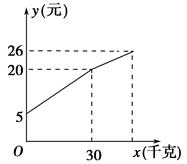

    (1) 农民自带的零钱是多少？
    (2) 降价前他每千克土豆出售的价格是多少？
    (3) 降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱(含备用零钱) 是26元，问他一共带了多少千克土豆．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，一次函数y1＝kx＋b的图象与反比例函数y2＝的图象相交于点A(2，3)和点B，与x轴相交于点C(8，0)．

    (1)求这两个函数的解析式；
    (2)当x取何值时，y1＞y2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（-4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．

    （1）求直线AB的函数解析式；
    （2）当点P在线段AB（不包括A，B两点）上时．
    ①求证：∠BDE=∠ADP；
    ②设DE=x，DF=y．请求出y关于x的函数解析式；
    （3）请你探究：点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，一次函数y1=x+1的图象与反比例函数（k为常数，且）的图象都经过点A(m,2).

    （1）求点A的坐标及反比例函数的解析式；
    （2）观察图象，当x>0时，直接写出y1与y2的大小关系.

    查看答案和解析>>

    同步练习册答案