
(12分)如图,已知反比例函数y= (k≠0)的图象经过点(
(k≠0)的图象经过点( ,8),直线y=-x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=-x+b经过该反比例函数图象上的点Q(4,m).
(1)求上述反比例函数和直线的函数表达式;
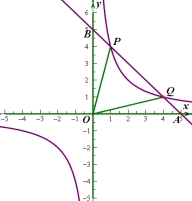
(2)设该直线与x轴、y轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
(1)y=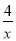 ;y=-x+5;(2)
;y=-x+5;(2) .
.
【解析】
试题分析:(1)首先根据点(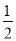 ,8)求出反比例函数的解析式,然后根据反比例函数解析式求出点Q的坐标,最后根据点Q的坐标求出一次函数解析式;(2)分别求出点A、点B、点P和点Q的坐标,让后将三角形的面积转化成△AOB的面积减去△BOP的面积减去△OAQ的面积.
,8)求出反比例函数的解析式,然后根据反比例函数解析式求出点Q的坐标,最后根据点Q的坐标求出一次函数解析式;(2)分别求出点A、点B、点P和点Q的坐标,让后将三角形的面积转化成△AOB的面积减去△BOP的面积减去△OAQ的面积.
试题解析:(1)由反比例函数的图象经过点(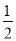 ,8),可知k=xy=
,8),可知k=xy=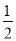 ×8=4,所以反比例函数解析式为y=
×8=4,所以反比例函数解析式为y=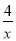 ,∵点Q是反比例函数和直线y=-x+b的交点,∴m=1,∴点Q的坐标是(4,1),∴b=x+y=5,
,∵点Q是反比例函数和直线y=-x+b的交点,∴m=1,∴点Q的坐标是(4,1),∴b=x+y=5,
∴直线的解析式为y=-x+5.
如图所示:由直线的解析式y=-x+5可知与x轴和y轴交点坐标点A与点B的坐标分别为(5,0)(0,5),由反比例函数与直线的解析式:y=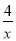 ,y=-x+5
,y=-x+5
可知两图像的交点坐标分别点P(1,4)和点Q(4,1),过点P作PC⊥y轴,垂足为C,过点Q作QD⊥x轴,垂足为D,
∴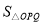 =
=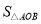 -
-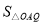 -
-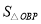 =
=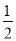 ×5×5-
×5×5-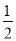 ×5×1-
×5×1-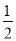 ×5×1=
×5×1= .
.
考点:反比例函数与一次函数.
考点分析: 考点1:一次函数 函数的定义: (k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。
(k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。  ,所以反比例函数可以写成
,所以反比例函数可以写成 的形式,自变量x的次数为-1;
的形式,自变量x的次数为-1;  ,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。
,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。 自变量的取值范围:
自变量的取值范围: (k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
试题属性
(k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
试题属性


科目:初中数学 来源:2014-2015学年山东省滨州市九年级下学期4月模拟数学试卷(解析版) 题型:选择题
如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )

A.28° B.52° C.62° D.72°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滨州市九年级下学期4月模拟数学试卷(解析版) 题型:选择题
若一次函数y=(m-3)x+5的函数值y随x的增大而增大,则 ( )
A.m>0 B.m<0 C.m>3 D.m<3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省东港市九年级九校联考数学试卷(解析版) 题型:填空题
如图,AB是⊙O的直径,点C、D都在⊙O上,若∠C=20°,则∠ABD的度数等于 .
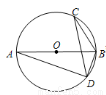
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市片九年级3月月考数学试卷(解析版) 题型:解答题
(本题满分8分)有3个完全相同的小球,把它们分别标号为1,2,3,放在一个口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球.
(1)采用树形图法(或列表法)列出两次摸球出现的所有可能结果;
(2)求摸出的两个球号码之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片九年级下学期第一次月考数学试卷(解析版) 题型:选择题
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( )
A.m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com