
【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A、B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 10 | 2000 |
10 | 5 | 2500 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2 , 室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台?
【答案】
(1)解:设每台A型空气净化器的销售利润为x元,每台B型空气净化器的销售利润为y元,
根据题意得: ![]() ,
,
解得: ![]() .
.
答:每台A型空气净化器的销售利润为200元,每台B型空气净化器的销售利润为100元.
(2)解:设购进A型空气净化器m台,则购进B型空气净化器(100﹣m)台,
∵B型空气净化器的进货量不少于A型空气净化器的2倍,
∴100﹣m≥2m,
解得:m≤ ![]() .
.
设销售完这100台空气净化器后的总利润为w元,
根据题意得:w=200m+100(100﹣m)=100m+10000,
∴w的值随着m的增大而增大,
∴当m=33时,w取最大值,最大值=100×33+10000=13300,此时100﹣m=67.
答:为使该公司销售完这100台空气净化器后的总利润最大,应购进A型空气净化器33台,购进B型空气净化器67台.
(3)解:设应购买A型空气净化器a台,则购买B型空气净化器(5﹣a)台,
根据题意得: ![]() [300a+200(5﹣a)]≥200×3,
[300a+200(5﹣a)]≥200×3,
解得:a≥2.
答:至少要购买A型空气净化器2台.
【解析】(1)等量关系式是:5台A型空气净化器的利润+10台A型空气净化器的利润=2000;10台A型空气净化器的利润+5台A型空气净化器的利润=2500,设未知数,建立方程组,求解即可。
(2)根据B型空气净化器的进货量不少于A型空气净化器的2倍,建立不等式,求出其解集,再列出总利润与m的函数关系式,根据一次函数的性质,即可求出其进货方案。
(3)根据已知建立不等式,求出解集,再求出a的最小整数解。
【考点精析】利用一元一次不等式的解法对题目进行判断即可得到答案,需要熟知步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )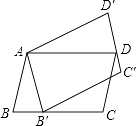
A.100°
B.105°
C.115°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区积极创建环保示范社区,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知温馨提示牌的单价为每个30元,垃圾箱的单价为每个90元,共需购买温馨提示牌和垃圾箱共100个.
(1)若规定温馨提示牌和垃圾箱的个数之比为1:4,求所需的购买费用;
(2)若该小区至多安放48个温馨提示牌,且费用不超过6300元,请列举所有购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,过点
,过点![]() 画
画![]() 轴的垂线
轴的垂线![]() ,点
,点![]() 在线段
在线段![]() 上,连结
上,连结![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,过点
,过点![]() 画
画![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)求![]() 的度数,并直接写出直线
的度数,并直接写出直线![]() 的解析式;
的解析式;
(2)若点![]() 的横坐标为2,求
的横坐标为2,求![]() 的长;
的长;
(3)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
图1

图2

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校2400名学生的阅读兴趣,从中随机抽查了部分同学,就“我最感兴趣的书籍”进行了调查:A.小说、B.散文、C.科普、D.其他(每个同学只能选择一项),进行了相关统计,整理并绘制出两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
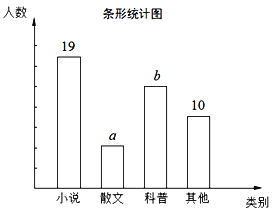

(1)本次抽查中,样本容量为______;
(2)a=______,b=______;
(3)扇形统计图中,其他类书籍所在扇形的圆心角是______°;
(4)请根据样本数据,估计全校有多少名学生对散文感兴趣.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com