
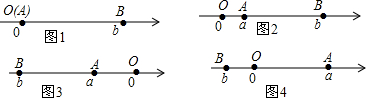
分析 根据两点间的距离是大数减小数,可得答案;
根据两点间的距离是两坐标间的绝对值,可得答案;
根据线段上的点到线段两短点的距离相等,可得答案.
解答 解:①数轴上表示2和5的两点之间的距离是5-2=3;
数轴上表示-2和-5的两点之间的距离是-2-(-5)=3;
数轴上表示1和-3的两点之间的距离是1-(-3)=1+3=4
②数轴上表示x和-1的两点A和B之间的距离是|x+1|,
如果|AB|=2,|x+1|=2,解得
x=1或x=-3;
【拓展提升】
③当代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2;
④当x=-2或3时,|x+1|+|x-2|=5.
故答案为:-1≤x≤2;-2或3.
点评 本题考查了实数与数轴,数轴上两点间的距离是坐标差的绝对值.


科目:初中数学 来源: 题型:解答题
 如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com