
 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数. 分析 首先根据三角形的内角和定理求得∠ACB的度数,以及∠BCD的度数,根据角的平分线的定义求得∠BCE的度数,则∠ECD可以求解,然后在△CDF中,利用内角和定理即可求得∠CDF的度数.
解答 解:∵∠A=30°,∠B=70°,
∴∠ACB=180°-∠A-∠B=80°.
∵CE平分∠ACB,
∴∠ACE=$\frac{1}{2}$∠ACB=40°.
∵CD⊥AB于D,
∴∠CDA=90°,
∠ACD=180°-∠A-∠CDA=60°.
∴∠ECD=∠ACD-∠ACE=20°.
∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF=180°-∠CFD-∠ECD=70°.
点评 本题考查了三角形的内角和等于180°以及角平分线的定义,是基础题,准确识别图形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 200名学生是总体 | B. | 200名学生是一个样本 | ||
| C. | 每个学生是个体 | D. | 全县七年级学生的体重是总体 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
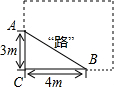 如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.
如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
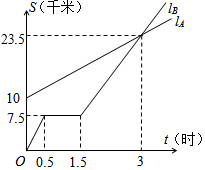 如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
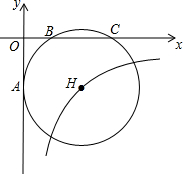 如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则反比例函数的解析式为-8$\sqrt{3}$.
如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则反比例函数的解析式为-8$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1+a不是一个代数式 | |
| B. | 0是一个单项式 | |
| C. | 一个多项式的次数为5,那么这个多项式的各项的次数都小于5 | |
| D. | 单项式-$\frac{2πa{b}^{2}}{3}$的系数是-$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com