
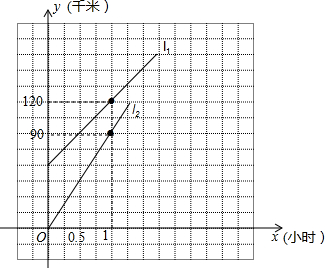
 Õıæ≠¿Ì¥”∞Ïπ´ “≥ÀA≥µ»•ƒ≥ –≤Œº”ª·“È£¨ø™≥µ50∑÷÷”∫Û£¨∑¢œ÷”–“ª÷ÿ“™Œƒº˛“≈¬©‘⁄∞Ïπ´ “÷–£¨À˚¡¢º¥¥ÚµÁª∞Õ®÷™√ÿ È£¨»√À˚ƒ√◊≈Œƒº˛ø™≥µÀÕÕ˘ø™ª·µÿµ„£¨10∑÷÷”∫Û√ÿ È≥ÀB≥µø™ º∞¥Õıæ≠¿Ì≥À≥µ¬∑œþ◊∑∏œ£¨»ÁÕºÀ˘ 浃l1∫Õl2±Ì æA°¢B¡Ω≥µœý∂‘”⁄≥ˆ∑¢µÿµƒæý¿Îy£®«ß√◊£©”Î◊∑∏œ ±º‰x£®–° ±£©÷ƺ‰µƒπÿœµ£∫
Õıæ≠¿Ì¥”∞Ïπ´ “≥ÀA≥µ»•ƒ≥ –≤Œº”ª·“È£¨ø™≥µ50∑÷÷”∫Û£¨∑¢œ÷”–“ª÷ÿ“™Œƒº˛“≈¬©‘⁄∞Ïπ´ “÷–£¨À˚¡¢º¥¥ÚµÁª∞Õ®÷™√ÿ È£¨»√À˚ƒ√◊≈Œƒº˛ø™≥µÀÕÕ˘ø™ª·µÿµ„£¨10∑÷÷”∫Û√ÿ È≥ÀB≥µø™ º∞¥Õıæ≠¿Ì≥À≥µ¬∑œþ◊∑∏œ£¨»ÁÕºÀ˘ 浃l1∫Õl2±Ì æA°¢B¡Ω≥µœý∂‘”⁄≥ˆ∑¢µÿµƒæý¿Îy£®«ß√◊£©”Î◊∑∏œ ±º‰x£®–° ±£©÷ƺ‰µƒπÿœµ£∫| 20 |
| 9 |
| 10 |
| 3 |
| 10 |
| 3 |
| 20 |
| 9 |
| 1 |
| 9 |
| 1 |
| 9 |



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
| (x+1)(x+2) |
| x2+4x+4 |
| 3x+6 |
| 2x2-8 |
| 1 |
| x2-4 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 1 |
| 1°¡2 |
| 1 |
| 2 |
| 1 |
| 2°¡3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3°¡4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1°¡2 |
| 1 |
| 2°¡3 |
| 1 |
| 3°¡4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2014)(b+2014) |
| 1 |
| 100°¡101 |
| 1 |
| 101°¡102 |
| 1 |
| n(n+1) |
| 1 |
| 2°¡4 |
| 1 |
| 4°¡6 |
| 1 |
| 6°¡8 |
| 1 |
| 2012°¡2014 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com