
【题目】在△ABC中,AB=AC,BD=CD,∠BAD=40°,AD=AE.求∠CDE的度数. 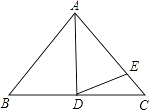
【答案】解:∵AB=AC,
∴△ABC为等腰三角形,
∵AD=AE,
∴△ADE为等腰三角形,
∵∠BAD=40°,
∴∠DAE=40°,
∴∠ADE= ![]() (180°﹣∠DAE)=
(180°﹣∠DAE)= ![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
又∵△ABC为等腰三角形,BD=CD,
∴AD⊥CD(三线合一),
∴∠CDE=90°﹣∠ADE=90°﹣70°=20°.
故答案为:20°
【解析】首先得到△ABC,△ADE均为等腰三角形,再根据等腰三角形的性质求解.
【考点精析】通过灵活运用三角形的内角和外角,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AC=BD时,它是矩形B.当AC⊥BD时,它是菱形
C.当∠A=60°时,它是菱形D.当AB=BC,AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的序号为( ) 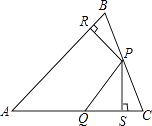
A.①②③
B.①②④
C.②③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况: 
(1)将下面的表格补充完整:
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:
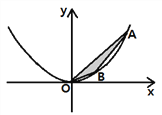
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题:
探究:当a=1时,
mn | m | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
归纳证明:
对任意m、n(m>n>0),猜想S=_________________ (用a,m,n表示),并证明你的猜想.
拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=____ (用a, m,n表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
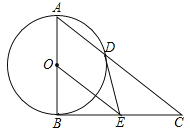
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CDOE;
(3)若![]() ,求OE的长.
,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com