
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)

【答案】楼房AB的高度为(35+10![]() )米.
)米.
【解析】试题分析:过点E作EF⊥BC于点F.在Rt△CEF中,求出CF=![]() EF,过点E作EH⊥AB于点H.在Rt△AHE中,∠HAE=45°,得到CF的值,再根据AB=AH+BH,求出AB的值.
EF,过点E作EH⊥AB于点H.在Rt△AHE中,∠HAE=45°,得到CF的值,再根据AB=AH+BH,求出AB的值.
试题解析:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
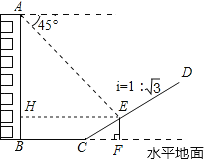
在Rt△CEF中,
∵i=![]() =tan∠ECF,
=tan∠ECF,
∴∠ECF=30°,
∴EF=![]() CE=10米,CF=10
CE=10米,CF=10![]() 米,
米,
∴BH=EF=10米,HE=BF=BC+CF=(25+10![]() )米,
)米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(25+10![]() )米,
)米,
∴AB=AH+HB=(35+10![]() )米.
)米.
答:楼房AB的高为(35+10![]() )米.
)米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某县对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:


(1)样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在 4.6 以上(含 4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题12分)抛物线![]() 经过点A(-4,0),B(2,0)且与
经过点A(-4,0),B(2,0)且与![]() 轴交于点C.
轴交于点C.
(1)求抛物线的解析式;
(2)如图1,P为线段AC上一点,过点P作![]() 轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴子F点,M、N分别是![]() 轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米,则路灯的高为 米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com