
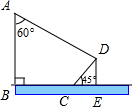
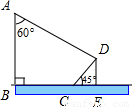
 如图,有一电线杆AB直立于地面,它的影子正好射在地面BC段和与地面成45°角的土坡CD上,已∠BAD=60°,BC=8米,
如图,有一电线杆AB直立于地面,它的影子正好射在地面BC段和与地面成45°角的土坡CD上,已∠BAD=60°,BC=8米, 米,求电线杆AB的高.(结果保留3个有效数字,
米,求电线杆AB的高.(结果保留3个有效数字, )
) 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
 如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:
如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
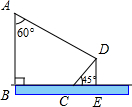 如图,有一电线杆AB直立于地面,它的影子正好射在地面BC段和与地面成45°角的土坡CD上,已∠BAD=60°,BC=8米,CD=2
如图,有一电线杆AB直立于地面,它的影子正好射在地面BC段和与地面成45°角的土坡CD上,已∠BAD=60°,BC=8米,CD=2| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
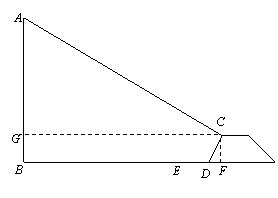
在电缆改造工程中,河岸边有一根电线杆AB(如图),河岸距电线杆AB水平距离是14米,即BD=14米,该河岸的坡面CD的坡度![]() 为
为![]() ,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(提示:在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域,
,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(提示:在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域,![]() )
)
查看答案和解析>>
科目:初中数学 来源:2010年吉林省吉林七中分校中考数学模拟试卷(周方民)(解析版) 题型:解答题
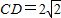 米,求电线杆AB的高.(结果保留3个有效数字,
米,求电线杆AB的高.(结果保留3个有效数字,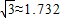 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com