
1.如图1,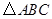 中,
中,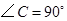 ,请用直尺和圆规作一条直线,把
,请用直尺和圆规作一条直线,把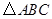 分割成两个等腰三角形(不写作法,但须保留作图痕迹).
分割成两个等腰三角形(不写作法,但须保留作图痕迹).
2.已知内角度数的两个三角形如图2、图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请画出直线并写出分割成的两个等腰三角形顶角的度数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3×4 | 2 |

查看答案和解析>>
科目:初中数学 来源:单科王牌 九年级数学(上) 题型:044
如图所示,是工人师傅用同一根不带刻度的直角尺作角平分线的示意图.
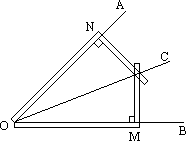
(1)你认为工人师傅这种作角平分线的方法正确吗?请说明理由.
(2)如图所示中,除了OC平分∠BOA外,你还有哪些结论?写出两个正确结论.
查看答案和解析>>
科目:初中数学 来源:新课标读想用 七年级数学(上)(北师大版) 题型:044
如图所示,一辆汽车在直线形公路AB上由A向B行驶,M、N分别是位于公路两侧的村庄.

(1)设汽车行驶到公路AB上点P位置时,距离村庄M最近;行驶到点Q位置时,距离村庄N最近,请在图中的公路AB上分别画出点P和点Q的位置.
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M、N两村庄都越来越近?在哪一段路上距离村庄N越来越近,而离村庄M越来越远?(分别用文字表述你的结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com