

���� ��1���������A��2��0����B��0��4����D��-4��0�����꣬�������߽���ʽΪy=a��x+4����x-2�����ѣ�0��4���������a���ɽ�����⣮
��2����ͼ2�У����������ٹ�Bƽ����CD��ֱ�߽��Գ�����Q1����ʱ�ı���ECBQ1��ƽ���ı��Σ���ֱ��AB��Գ���Ľ���M��-1��6����Q1����M�ĶԳƵ�Q2��-1�� $\frac{17}{2}$������Q2F2��EC��ֱ��AB��F2����֪�ı���ECQ2F2��ƽ���ı��Σ��ֱ������Q���꼴�ɣ�
��3����ͼ3�У�����OG��OH������֤����HOG�ǵ���ֱ�������Σ��Ƴ�OM=HM=GM��OG=OH=$\sqrt{2}$OM������OM=$\sqrt{10}$���Ƴ�OG=2$\sqrt{5}$��AB=4$\sqrt{5}$����B��0��m����A��$\frac{m}{2}$��0�����ɵ�m2+��$\frac{m}{2}$��2=��4$\sqrt{5}$��2���ⷽ�̼��ɽ�����⣮���ɢٿ�֪����HOG�ǵ���ֱ�������Σ���HOG������Ϊ��M����$\sqrt{2}$��m��4$\sqrt{2}$ʱ����M������OM���˶�����COM�Ƕ�ֵ��
���m=$\sqrt{2}$��4$\sqrt{2}$ʱ��OM��ֵ�����ɽ�����⣮
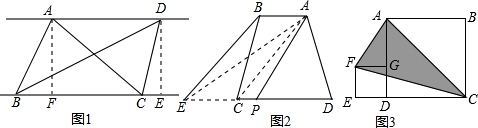
��� �⣺��1����ͼ1�У�
m=4ʱ��ֱ��l1�Ľ���ʽΪy=-2x+4��
��x=0��y=4����y=0��x=2��
��A��2��0����B��0��4����
�ߡ�DOC���ɡ�AOB��ת�õ���
��OC=OA=2��OD=OB=4��
��D��-4��0����C��0��2��
�������߽���ʽΪy=a��x+4����x-2�����ѣ�0��4������õ�a=-$\frac{1}{2}$��
�������߽���ʽΪy=-$\frac{1}{2}$x2-x+4��
��2����ͼ2�У�
y=-$\frac{1}{2}$x2+x+4=-$\frac{1}{2}$��x+1��2+$\frac{9}{2}$��
��Գ���Ϊx=1��
��ֱ��CD����ʽΪy=kx+b������ $\left\{\begin{array}{l}{b=2}\\{-4k+b=0}\end{array}\right.$��
��� $\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��CD����ʽΪy=$\frac{1}{2}$x+2��
��E��-1��$\frac{3}{2}$����
�ٹ�Bƽ����CD��ֱ�߽��Գ�����Q1����ʱ�ı���ECBQ1��ƽ���ı��Σ�
��ֱ��CD����ʽΪy=$\frac{1}{2}$x+2��B��0��4����
��ֱ��BQ1����ʽΪy=$\frac{1}{2}$x+4��
��Q1��-1��$\frac{7}{2}$����
��ֱ��AB��Գ���Ľ���M��-1��6����Q1����M�ĶԳƵ�Q2��-1�� $\frac{17}{2}$����
��Q2F2��EC��ֱ��AB��F2����֪�ı���ECQ2F2��ƽ���ı��Σ�
�������������Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı���ʱ����Q�����꣨-1��$\frac{7}{2}$����-1��$\frac{17}{2}$����
��3����ͼ3�У�����OG��OH��
��GΪAB�е㣬HΪCD�е㣬��COD=��AOB=90�㣬
��OG=$\frac{1}{2}$AB��OH=$\frac{1}{2}$CD��
��AB=CD��
��OG=OH��OH=DH��
��OG=GA��OH=DH��
���GOA=��OAB����HOD=��HDO��
�ߡ�ODC=��OBA����OBC+��OAB=90��
���HOD+��AOG=90�㣬
���HOG=90�㣬
���HOG�ǵ���ֱ�������Σ�
��HM=MG��
��OM=HM=GM��OG=OH=$\sqrt{2}$OM��
�١�OM=$\sqrt{10}$��
��OG=2$\sqrt{5}$��
��AB=4$\sqrt{5}$��
��B��0��m����A��$\frac{m}{2}$��0����
��m2+��$\frac{m}{2}$��2=��4$\sqrt{5}$��2��
��m��0��
��m=8��
��ֱ��l1�Ľ���ʽΪy=-2x+8��
���ɢٿ�֪����HOG�ǵ���ֱ�������Σ�
���HOG��������M��
��$\sqrt{2}$��m��4$\sqrt{2}$ʱ����M������OM���˶�����COM�Ƕ�ֵ��
��m=$\sqrt{2}$ʱ��B��0��$\sqrt{2}$����A��$\frac{\sqrt{2}}{2}$��0����
��AB=$\sqrt{��\sqrt{2}��^{2}+��\frac{\sqrt{2}}{2}��^{2}}$=$\frac{\sqrt{10}}{2}$��
��OG=$\frac{1}{2}$AB=$\frac{\sqrt{10}}{4}$��
��OM=$\frac{\sqrt{2}}{2}$OG=$\frac{\sqrt{5}}{4}$��
��m=4$\sqrt{2}$ʱ��ͬ���ɵ�OM=$\sqrt{5}$��
�൱$\sqrt{2}$��m��4$\sqrt{2}$ʱ����ֱ��д����HOG���ԲԲ���������˶����������߹���·�߳�=$\sqrt{5}$-$\frac{\sqrt{5}}{4}$=$\frac{3\sqrt{5}}{4}$��
���� ���⿼����κ����ۺ��⡢����ϵ������ƽ���ı��ε��ж������ʡ�ֱ��������б�����߶��������ɶ���������ֱ�������ε��ж������ʵ�֪ʶ������Ĺؼ������������Щ֪ʶ������⣬ѧ��������ۣ�����©�⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2016}$ | B�� | 2016 | C�� | -$\frac{1}{2016}$ | D�� | -2016 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com