
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,一农户要建一个矩形猪舍,猪舍的一边利用现有的住房墙,另外三边用25m长得建筑材料围成,为方便进出,在垂直于住房墙的一边留一个小门.
如图,一农户要建一个矩形猪舍,猪舍的一边利用现有的住房墙,另外三边用25m长得建筑材料围成,为方便进出,在垂直于住房墙的一边留一个小门.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
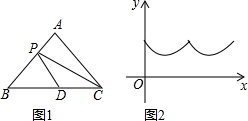 如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
如图1,在△ABC 中,AB=AC,点D是BC的中点,点P沿B→A→C方向从点B运动到点C.设点P经过的路径长为x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )| A. | BP | B. | AP | C. | DP | D. | CP |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 8 | C. | 4 | D. | 6. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某地下车库的入口处有斜坡CB,它的坡度为i=1:2.4,斜坡CB的长为13米.
如图,某地下车库的入口处有斜坡CB,它的坡度为i=1:2.4,斜坡CB的长为13米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com