
 .
.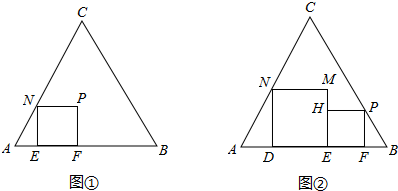
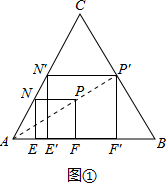 解:(1)如图①,正方形E′F′P′N′即为所求.
解:(1)如图①,正方形E′F′P′N′即为所求. x.
x. x+
x+ x=3+
x=3+ ,
, ,即x=3
,即x=3 -3,
-3,
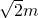 ,PE=
,PE= n.
n. PN2,
PN2, m+m+n+
m+m+n+ n=
n= +3,化简得m+n=3.
+3,化简得m+n=3. [32+(m-n)2]=
[32+(m-n)2]= +
+ (m-n)2
(m-n)2 ;
; -3.
-3. [9+(m最大-n最小)2]
[9+(m最大-n最小)2] [9+(3
[9+(3 -3-6+3
-3-6+3 )2]
)2] ….
…. ,S最小=
,S最小= .
. +
+ (m-n)2,可见S的大小只与m、n的差有关:
(m-n)2,可见S的大小只与m、n的差有关:

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
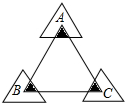 如图,正三角形ABC的边长为12,三个全等的小正三角形重心(即三条中线的交点)与正三角形ABC的顶点重合,且他们各有一边与正三角形ABC的一边平行.若小正三角形的边长为x,且0<x≤12,阴影部分的面积为S,则能反映S与x之间函数关系的大致图象是( )
如图,正三角形ABC的边长为12,三个全等的小正三角形重心(即三条中线的交点)与正三角形ABC的顶点重合,且他们各有一边与正三角形ABC的一边平行.若小正三角形的边长为x,且0<x≤12,阴影部分的面积为S,则能反映S与x之间函数关系的大致图象是( )A、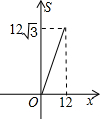 | B、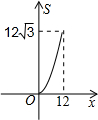 | C、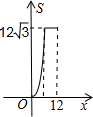 | D、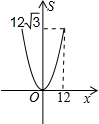 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| n | 1 | 2 | 3 | 4 |
| ln |
查看答案和解析>>
科目:初中数学 来源: 题型:
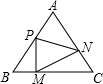 如图,正三角形ABC的边长为l,点M,N,P分别在边BC,AB上,设BM=x,CN=y,AP=z,且x+y+z=1.
如图,正三角形ABC的边长为l,点M,N,P分别在边BC,AB上,设BM=x,CN=y,AP=z,且x+y+z=1.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当
(2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当| 2 |
| π |
| 2 |
| 4π |
| 3 |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com