
 如图,OC是∠AOB内部的一条射线,且OM,ON分别平分∠AOC与∠BOC.
如图,OC是∠AOB内部的一条射线,且OM,ON分别平分∠AOC与∠BOC.分析 (1)根据角平分线的定义得到∠COM=$\frac{1}{2}$∠AOC,∠CON=$\frac{1}{2}$∠BOC,然后利用∠MON=∠MOC+∠CON即可得到结果;
(2)同理(1)可得∠MON=∠COM+∠CON=$\frac{1}{2}α+\frac{1}{2}β$,易得∠AOB=2∠MON.
解答 解:∵OM、ON分别平分∠AOC、∠BOC,
∴∠COM=$\frac{1}{2}$∠AOC=,∠CON=$\frac{1}{2}$∠BOC,
(1)当∠AOC=120°,∠BOC=30°,
∴∠MON=∠COM+∠CON=$\frac{1}{2}×120°+\frac{1}{2}×30°$=75°;
(2)当∠AOC=α,∠BOC=β,
∴∠MON=∠COM+∠CON=$\frac{1}{2}α+\frac{1}{2}β$,
∠AOB=2∠MON.
点评 本题考查了角度的计算,角平分线的定义,熟练掌握定义是解答此题的关键.


科目:初中数学 来源: 题型:解答题
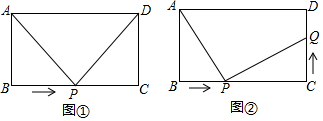
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
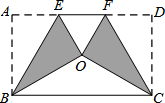 将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$.
将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
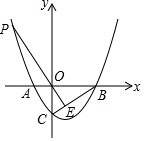 如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,点P为第二象限的抛物线上一点,且线PO交BC于E.
如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,点P为第二象限的抛物线上一点,且线PO交BC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com