
【题目】 如图, D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若![]() ,则四边形BEFD的面积为
,则四边形BEFD的面积为

A.5 B.7 C.9 D.10
【答案】B.
【解析】
试题解析:∵AD=2BD,S△ABC=30,
∴S△ADC=![]() S△ABC=20,S△BDC=
S△ABC=20,S△BDC=![]() S△ABC=10.
S△ABC=10.
过E作EG∥AB交CD于G,
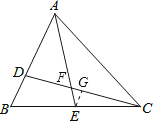
∵BE=CE,
∴CG=DG,
∴BD=2EG,
∵AD=2BD,
∴AD=4EG.
设S△EGF=x.
∵EG∥BD,
∴△CEG∽△CBD,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴S△CEG=![]() S△CBD=
S△CBD=![]() ×10=
×10=![]() ,S梯形EGDB=10-
,S梯形EGDB=10-![]() =
=![]() ,
,
设S△FEG=x,则S四边形BEFD=![]() -x,
-x,
∵S△ABE=![]() S△ABC=15,
S△ABC=15,
∴S△ADF=S△ABE-S四边形BEFD=(15-![]() -x)=
-x)=![]() +x.
+x.
∵EG∥AD,
∴△FEG∽△FAD,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴S△FAD=16S△FEG=16x,
∴16x=![]() +x,
+x,
解得x=![]() ,
,
∴S四边形BEFD=![]() -x=
-x=![]() -
-![]() =7.
=7.
故选B.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
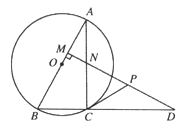
【题目】如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的ND边的中线.
(1)求证:△ABC≌△DNC;
(2)试判断CP与⊙O的位置关系,并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com