
| 1 |
| 2 |
| 1 |
| 2 |
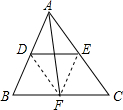 (1)证明:连接DF,EF,
(1)证明:连接DF,EF,| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
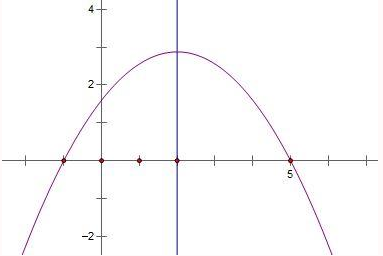 已知y=ax2+bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:
已知y=ax2+bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
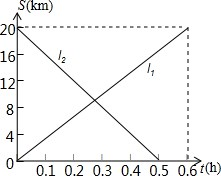 甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表 示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系.
甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表 示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系. 查看答案和解析>>
科目:初中数学 来源: 题型:
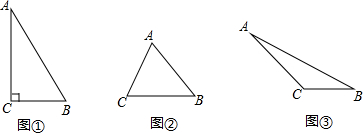
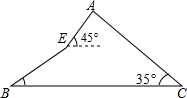 如图所示,甲、乙两班学生进行爬山比赛,甲班学生从西坡沿坡角为30°的山坡爬了200米,紧接着又爬了坡角为45°的山坡80米,最后到达山顶;乙班学生从东坡沿着坡角为35°的斜坡爬向山顶,若两班学生爬山的平均速度相同,请问哪班学生先到达山顶.(结果精确到个位,参考数据:
如图所示,甲、乙两班学生进行爬山比赛,甲班学生从西坡沿坡角为30°的山坡爬了200米,紧接着又爬了坡角为45°的山坡80米,最后到达山顶;乙班学生从东坡沿着坡角为35°的斜坡爬向山顶,若两班学生爬山的平均速度相同,请问哪班学生先到达山顶.(结果精确到个位,参考数据:| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com