练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．如图，四边形ABCD内接于圆，则图中与∠ABD相等的角是（　　）
    A．∠CADB．∠ACDC．∠CBDD．∠ACB

    分析 根据圆周角定理解得即可．

    解答 解：∵∠ABD和∠ACD所对的弧都是$\widehat{AD}$，
    根据圆周角定理得：∠ABD=∠ACD，
    故选：B．

    点评 本题考查的是圆周角定理的应用，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．在进行异号的两个有理数加法运算时，用到下面的一些操作：
    ①将绝对值较大的有理数的符号作为结果的符号并记住
    ②将记住的符号和绝对值的差一起作为最终的计算结果
    ③用较大的绝对值减去较小的绝对值
    ④求两个有理数的绝对值
    ⑤比较两个绝对值的大小
    其中操作顺序正确的步骤是（　　）
    A．①②③④⑤B．④⑤③②①C．①⑤③④②D．④⑤①③②

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

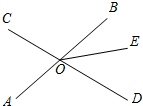    16．如图，直线AB、CD相交于点O，∠AOC=72°，射线OE在∠BOD的内部，∠DOE=2∠BOE．
    （1）求∠BOE和∠AOE的度数；
    （2）若射线OF与OE互相垂直，请直接写出∠DOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯，已知两个陌生人在1至3层的任意一层出电梯．
    （1）请用画树状图或列表的方法，求出甲、乙二人在同一楼层出电梯的概率；
    （2）小亮和小芳打赌说：“若甲、乙二人在相邻楼层出电梯，则小亮胜，否则小芳胜”．该游戏是否公平？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．程大位所著《算法统宗》是一部中国传统数学重要的著作．在《算法统宗》中记载：“平地秋千未起，踏板离地一尺．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几？”【注释】1步=5尺．
    译文：“当秋千静止时，秋千上的踏板离地有1尺高，如将秋千的踏板往前推动两步（10尺）时，踏板就和人一样高，已知这个人身高是5尺．美丽的姑娘和才子们，每天都来争荡秋千，欢声笑语终日不断．好奇的能工巧匠，能算出这秋千的绳索长是多少吗？”
    如图，假设秋千的绳索长始终保持直线状态，OA是秋千的静止状态，A是踏板，CD是地面，点B是推动两步后踏板的位置，弧AB是踏板移动的轨迹．已知AC=1尺，CD=EB=10尺，人的身高BD=5尺．设绳索长OA=OB=x尺，则可列方程为102+（x-5+1）2=x2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．菱形的边长为5，一条对角线长为8，则此菱形的面积是（　　）
    A．24B．30C．40D．48

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某同学报名参加学校秋季运动会，有以下5个项目可供选择：径赛项目：100m、200m、1000m（分别用A1、A2、A3表示）；田赛项目：跳远，跳高（分别用T1、T2表示）．
    （1）该同学从5个项目中任选一个，恰好是田赛项目的概率P为$\frac{2}{5}$；
    （2）该同学从5个项目中任选两个，求恰好是一个径赛项目和一个田赛项目的概率P1，利用列表法或树状图加以说明；
    （3）该同学从5个项目中任选两个，则两个项目都是径赛项目的概率P2为$\frac{3}{10}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，四边形ABCD内接于⊙O，∠BCD=120°，则∠BAD的度数是（　　）
    A．30°B．60°C．80°D．120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．若|a|=3，|b|=1，则代数式a+b的值是（　　）
    A．4B．-4C．2或-2D．±2或±4

    查看答案和解析>>

    同步练习册答案