练习册

  • 练习册
  • 试题
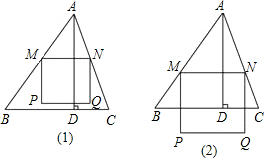
    精英家教网 > 初中数学 > 题目详情
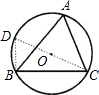    锐角△ABC中，BC=6，S△ABC=12，两动点M、N分别在边AB、AC上滑动，且精英家教网MN∥BC，以MN为边向下作正方形MPQN，设其边长为x，正方形MPQN与△ABC公共部分的面积为y（y＞0）．
    （1）求y与x的函数关系和自变量x的取值范围；
    （2）求当x为何值时，y的值最大，并求y的最大值．
    分析：（1）根据正方形和长方形的面积公式，即可求出y与x的函数关系；
    （2）根据（1）的函数关系式，结合自变量x的取值范围，分情况讨论，求出y的最大值．
    解答：解：（1）当0＜x≤2.4时，y=x2（3分）
    当2.4＜x＜6时，y=-
    2
    3
    x2+4x    ；（3分）

    （2）在0＜x≤2.4时，
    ∴当x取最大值2.4时，y有最大值=x2=2.4×2.4=5.76．
    当2.4＜x＜6时，y=-
    2
    3
    x2+4x    ，
    y=-
    2
    3
    (x-3)2+6    ，
    当x=3时，y最大值=6．
    所以，当x=3时，y最大值=6．（4分）
    点评：本题综合考查函数的知识．确定二次函数的最值时，首先看自变量的取值范围，当自变量取全体实数时，其最值为抛物线顶点坐标的纵坐标；当自变量取某个范围时，要分别求出顶点和函数端点处的函数值，比较这些函数值，从而获得最值．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    精英家教网阅读材料，解答问题：
    命题：如图，在锐角△ABC中，BC=a，CA=b，AB=c，△ABC的外接圆半径为R，则
    a
    sinA
    =
    b
    sinB
    =
    c
    sinC
    =2R．
    证明：连接CO并延长交⊙O于点D，连接DB，则∠D=∠A．
    因为CD是⊙O的直径，所以∠DBC=90°，
    在Rt△DBC中，sin∠D=
    BC
    DC
    =
    a
    2R
    ，
    所以sinA=
    a
    2R
    ，即
    a
    sinA
    =2R，
    同理：
    b
    sinB
    =2R，
    c
    sinC
    =2R，
    a
    sinA
    =
    b
    sinB
    =
    c
    sinC
    =2R，
    请阅读前面所给的命题和证明后，完成下面（1）（2）两题：
    （1）前面阅读材料中省略了“
    b
    sinB
    =2R，
    c
    sinC
    =2R”的证明过程，请你把“
    b
    sinB
    =2R”的证明过程补写出来．
    （2）直接运用阅读材料中命题的结论解题，已知锐角△ABC中，BC=
    		3
    ，CA=
    		2
    ，∠A=60°，求△ABC的外接圆半径R及∠C．
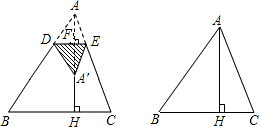    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在锐角△ABC中，BC=9，AH⊥BC于点H，且AH=6，点D为AB边上的任意一点，过点D作DE∥BC，交AC于点E．设△ADE的高AF为x（0＜x＜6），以DE为折线将△ADE翻折，所得的△A′DE与梯形DBCE重叠部分的面积记为y（精英家教网点A关于DE的对称点A′落在AH所在的直线上）．
    （1）当x=1时，y=
     
    ；
    （2）求出当0＜x≤3时，y与x的函数关系式；
    （3）求出3＜x＜6时，y与x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在锐角△ABC中，BC=6，∠A=60°，则△ABC外接圆的直径为
    4
    		3
    4
    		3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在锐角△ABC中，BC=9，AH⊥BC于点H，且AH=6，点D为AB边上的任意一点，过点D作DE∥BC，交AC于点E．设△ADE的高AF为x（0＜x＜6），以DE为折线将△ADE翻折，所得的△A'DE与梯形DBCE重叠部分的面积记为y（点A关于DE的对称点A'落在AH所在的直线上）．
    （1）分别求出当0＜x≤3与3＜x＜6时，y与x的函数关系式；
    （2）当x取何值时，y的值最大，最大值是精英家教网多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在面积为75cm2的锐角△ABC中，BC=15cm，从这张硬纸片上剪下一个正方形DEFG，使它的一边EF在BC上，顶点D、G分别在AB，AC上．求这个正方形的边长？

    查看答案和解析>>

    同步练习册答案