
【题目】正方形ABCD的一条对角线长为8,则这个正方形的面积是( )
A.4![]()
B.32
C.64
D.128
【答案】B
【解析】解:在正方形中,对角线相等,所以正方形ABCD的对角线长均为8,
∵正方形又是菱形,
菱形的面积计算公式是S=![]() ab(a、b是正方形对角线长度)
ab(a、b是正方形对角线长度)
∴S=![]() ×8×8=32,
×8×8=32,
故选B.
【考点精析】关于本题考查的正方形的性质和概率公式,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
![]() ,
,![]() ,
,![]() ,…
,…
![]() 根据上述格式反应出的规律填空:
根据上述格式反应出的规律填空:![]() ________;
________;
![]() 设这类等式左边两位数的十位数字为
设这类等式左边两位数的十位数字为![]() ,请用一个含
,请用一个含![]() 的代数式表示其结果;
的代数式表示其结果;
![]() 这种简便计算也可以推广应用:个位数字是
这种简便计算也可以推广应用:个位数字是![]() 的三位数的平方,请写出
的三位数的平方,请写出![]() 的简便计算过程及结果.
的简便计算过程及结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线l1:y=![]() (x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
A.y=![]() (x﹣2)2+4
(x﹣2)2+4
B.y=![]() (x﹣2)2+3
(x﹣2)2+3
C.y=![]() (x﹣2)2+2
(x﹣2)2+2
D.y=![]() (x﹣2)2+1
(x﹣2)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC折叠,使B落在E处,AE交CD于点F,则下列结论中不一定成立的是( )
A.AD=CE
B.AF=CF
C.△ADF≌△CEF
D.∠DAF=∠CAF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形.
(2)若AB=6,BC=8,求四边形OCED的周长.
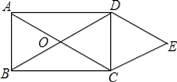
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=![]() ,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
(1)求证:∠EDB=∠B.
(2)若sinB=![]() ,AB=10,OA=2,求线段DE的长.
,AB=10,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(8,4),点B(0,4),线段CD的长为3,点C与原点O重合,点D在x轴正半轴上.线段CD沿x轴正方向以每秒1个单位长度的速度向右平移,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F(如图2),设运动时间为t.当E点与A点重合时停止运动.
(1)求线段CE的长;
(2)记△CDE与△ABO公共部分的面积为S,求S关于t的函数关系式;
(3)如图2,连接DF.
①当t取何值时,以C、F、D为顶点的三角形为等腰三角形?
②△CDF的外接圆能否与OA相切?如果能,直接写出此时t的值;如果不能,请说明理由.

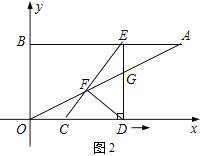
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )

A. 30 B. 34 C. 36 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示: (1)按下列语句画出图形:
①延长AC到D,使CD=AC;②反向延长CB到E,使CE=BC;③连接DE.
(2)度量其中的线段和角,你有什么发现?
(3)试判断图中两个三角形的面积是否相等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com