
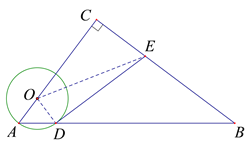
【题目】如图,在△ABC中,∠C=![]() ,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
(1)求证:∠EDB=∠B.
(2)若sinB=![]() ,AB=10,OA=2,求线段DE的长.
,AB=10,OA=2,求线段DE的长.

【答案】(1)见解析;(2)4.75
【解析】分析:(1)、连接OD,根据切线的性质得出∠ODA+∠EDB=![]() ,根据三角形内角和定理得出∠A+∠B=
,根据三角形内角和定理得出∠A+∠B=![]() ,根据OA=OD得出∠A=∠ODA,从而得出答案;(2)、连接OE,根据三角函数得出AC的长度,根据勾股定理得出BC的值,设DE=x,则BE=DE=x,CE=8-x,根据
,根据OA=OD得出∠A=∠ODA,从而得出答案;(2)、连接OE,根据三角函数得出AC的长度,根据勾股定理得出BC的值,设DE=x,则BE=DE=x,CE=8-x,根据![]() 得出答案.
得出答案.
详解:(1)解:连结OD,
∵DE与⊙O相切于点D,∴OD⊥DE. ∴∠ODE=![]() . ∴∠ODA+∠EDB=
. ∴∠ODA+∠EDB=![]() .
.
∵∠C=![]() , ∴∠A+∠B=
, ∴∠A+∠B=![]() . ∵OA=OD, ∴∠A=∠ODA. ∴∠EDB=∠B.
. ∵OA=OD, ∴∠A=∠ODA. ∴∠EDB=∠B.
(2)连结OE, ∵∠EDB=∠B, ∴EB=ED. ∵AB=10,sinB=![]() =
=![]() , ∴AC=6.
, ∴AC=6.
由勾股定理,得BC=8. 设DE=x,则EB=ED=x,CE=8-x.
∵∠C=∠ODE =![]() , ∴
, ∴![]() .
.
∴![]() , ∴
, ∴![]() , 即DE=
, 即DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点C的坐标为(﹣1,1),将Rt△ABC按一定的规律变换:第一次,将Rt△ABC沿AC边翻折,得Rt△AB1C;第二次,将Rt△AB1C绕点B1逆时针旋转90°,得Rt△A1B1C1;第三次,将Rt△A1B1C1沿A1C1边翻折,得Rt△A1B2C1;第四次,将Rt△A1B2C1绕点B2逆时针90°,得Rt△A2B2C2…如此依次下去
(1)试在图中画出Rt△A1B1C1和Rt△A2B2C2 , 并写出A1的坐标 ;
(2)请直接写出在第11次变换后所得的点B的对应的点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是面积为1的等边三角形。取BC边中点E,作ED∥AB,
EF∥AC,得到四边形EDAF,它的面积记做S1;取BE中点G,做GH∥FB,GK∥EF,
得到四边形GHFK,它的面积记作S2.照此规律作下去,
则S2018=__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校假期由校长带领该校“三好学生”去旅游,甲旅行社说“若校长买全票一张,则学生半价.”乙旅行社说“全部人六折优惠”若全票价是1200元,则:
(1)若学生人数是20人,甲、乙旅行社收费分别是多少?
(2)当学生人数的多少时,两家旅行社的收费一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班现要从A、B两位男生和D、E两位女生中,选派学生代表本班参加全校“中华好诗词”大赛.
(1)如果选派一位学生代表参赛,那么选派到的代表是A的概率 ;
(2)如果选派两位学生代表参赛,求恰好选派一男一女两位同学参赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,O为坐标原点,横、纵轴的单位长度相同,A、B的坐标分别为(8,6),(16,0),点P沿OA边从点O开始向终点A运动,速度每秒1个单位,点Q沿BO边从B点开始向终点O运动,速度每秒2个单位,如果P、Q同时出发,用t(秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动。求:

(1)几秒时PQ∥AB.
(2)设△OPQ的面积为y,求y与t的函数关系式.
(3)△OPQ与△OAB能否相似?若能,求出点P的坐标,若不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com