
【题目】如图,△ABC是面积为1的等边三角形。取BC边中点E,作ED∥AB,
EF∥AC,得到四边形EDAF,它的面积记做S1;取BE中点G,做GH∥FB,GK∥EF,
得到四边形GHFK,它的面积记作S2.照此规律作下去,
则S2018=__________________.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图中的图象(折线![]() )描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为![]() 千米/时;
千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是 米.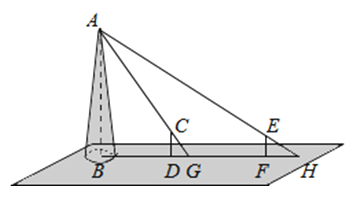
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥GD,∠1=∠2,∠BAC=65°.将求∠AGD的过程填写完整.
∵EF∥CD,
∴∠2= ( ),
∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( ),
∴∠BAC+ =180°( ),
∵∠BAC=65°,
∴∠AGD= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线l1:y=![]() (x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
A.y=![]() (x﹣2)2+4
(x﹣2)2+4
B.y=![]() (x﹣2)2+3
(x﹣2)2+3
C.y=![]() (x﹣2)2+2
(x﹣2)2+2
D.y=![]() (x﹣2)2+1
(x﹣2)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形.请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC折叠,使B落在E处,AE交CD于点F,则下列结论中不一定成立的是( )
A.AD=CE
B.AF=CF
C.△ADF≌△CEF
D.∠DAF=∠CAF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=![]() ,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
(1)求证:∠EDB=∠B.
(2)若sinB=![]() ,AB=10,OA=2,求线段DE的长.
,AB=10,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1,﹣2);
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
(4)若图中另有两个格点M、N,且M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),则N→A应记为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com