
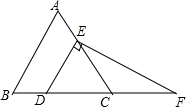
如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,
(1)求∠F的度数;
(2)若CD=3,求DF的长.
【考点】等边三角形的判定与性质.
【分析】(1)根据平行线的性质可得∠EDC=∠B=60°,根据三角形内角和定理即可求解;
(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.
【解答】解:(1)∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°﹣∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形.
∴ED=DC=3,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=6.
【点评】本题考查了等边三角形的判定与性质,以及直角三角 形的性质,30度的锐角所对的直角边等于斜边的一半.
形的性质,30度的锐角所对的直角边等于斜边的一半.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
点P(﹣2,﹣3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )
A.(﹣3,0) B.(﹣1,6) C.(﹣3,﹣6) D.(﹣1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图:某地有两所大学和两条相交叉的公路(点M,N表示大学,AO,BO表示公路).现计划修建一座仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案(要求保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是__________海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
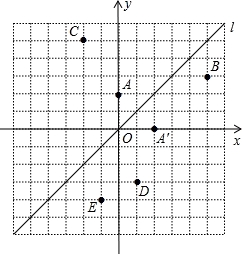
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′__________、C′__________;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为__________(不必证明);
运用与拓广:
(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com