
【题目】如图,已知BC=DE,∠BCF=∠EDF,AF垂直平分CD.求证:∠B=∠E. 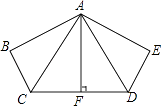
【答案】证明: ∵AF垂直平分CD,
∴AC=AD,∠ACD=∠ADC,
∵∠BCF=∠EDF,
∵∠BCF﹣∠ACD=∠EDF﹣∠ADC,
∴∠BCA=∠EDA,
在△ABC和△AED中 ,
,
∴△ABC≌△AED(SAS),
∴∠B=∠E.
【解析】由已知条件和垂直平分线的性质易证∠BCA=∠EDA,再结合全等三角形的判断方法即可证明△ABC≌△AED,由全等三角形的性质:对应角相等即可得到∠B=∠E.
【考点精析】利用线段垂直平分线的性质对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列现象中不属于平移的是( )
A. 滑雪运动员在平坦的雪地上滑雪 B. 彩票大转盘在旋转
C. 高楼的电梯在上上下下 D. 火车在一段笔直的铁轨上行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
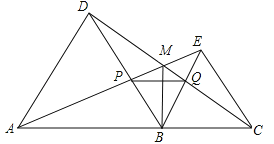
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() ;④S△ABC=4S△ADF.其中正确的有( )
;④S△ABC=4S△ADF.其中正确的有( )
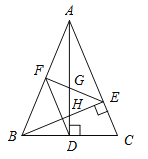
A.1个 B.2 个 C.3 个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
A.32,31
B.31,32
C.31,31
D.32,35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,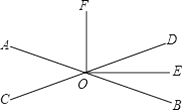
(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是 时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是 时,它们一定不全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com