

分析 (1)分别令x=0,y=0,即可求出点A,B的坐标,由抛物线b=0,可知对称轴为y轴;
(2)根据相切,可知AB、CD距离是$\frac{1}{2}$AB=$\frac{5}{2}$,利用平行四边形的面积,求出AC的长度,利用抛物线平移即可求出平移后的解析式;
(3)根据题意,可知△PNC≌△C′QP,利用全等三角形的对应线段相等,用含n的式子表示出点C′的坐标,由于点C′在抛物线上,将其坐标代入抛物线解析式,求解即可.
解答 解:(1)∵抛物线解析式为:y=$-\frac{4}{9}{x}^{2}+4$,
∴对称轴为y轴,
令y=0,得:$-\frac{4}{9}{x}^{2}+4$=0,解得:x=±3,
∵点A在x轴的正半轴上,
∴点A(3,0),
令x=0,得:y=4,
∴点B的坐标为(0,4);
(2)由OA=3,OB=4,可得AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵CD与⊙M相切,
∴点B到CD的距离d等于$\frac{1}{2}$AB=$\frac{5}{2}$,
连接BD,如图1,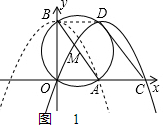
∴S平行四边形ABCD=AB•d=AC×4,
∴AC=$\frac{25}{8}$,
∴移动后的抛物线解析式为:y=$-\frac{4}{9}(x-\frac{25}{8})^{2}+4$;
(3)如图2,设P($\frac{25}{8}$,n),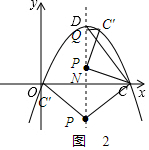
过点C′Q⊥PD,设对称轴与x轴交于点N.
∴△PNC≌△C′QP,
∴C′Q=PN,PQ=NC,
∵抛物线y=$-\frac{4}{9}(x-\frac{25}{8})^{2}+4$与x轴的交点为($\frac{1}{8}$,0),($\frac{49}{8}$,0),
∴C′Q=PN=n,PQ=NC=3,
∴C′($\frac{25}{8}$+n,n+3),
∵C′($\frac{25}{8}$+n,n+3)在抛物线y=$-\frac{4}{9}(x-\frac{25}{8})^{2}+4$上,
∴n+3$-\frac{4}{9}(x-\frac{25}{8})^{2}+4$,解得:n1=$\frac{3}{4}$,n2=-3,
∴P1($\frac{25}{8}$,$\frac{3}{4}$),P2($\frac{25}{8}$,-3).
点评 本题主要考查二次函数及旋转的图形变形,解决第(3)小题时,能够找到线段旋转后,有两个三角形全等,进而确定出点C′的坐标是解决此题的关键,解决此类问题要灵活运用前面学过的知识.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.
如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
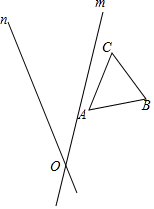 如图,直线m,n的夹角为35°,相交于点O,
如图,直线m,n的夹角为35°,相交于点O,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com