
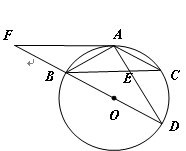
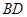 为⊙
为⊙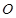 的直径,
的直径,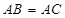 ,
,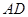 交
交 于点
于点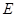 ,
,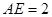 ,
,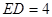 .
.
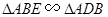 ;
;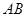 的长;
的长;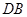 到
到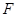 ,使得
,使得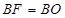 ,连接
,连接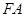 ,试判断直 线
,试判断直 线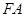 与⊙
与⊙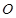 的位置关系,并说明理由.
的位置关系,并说明理由. 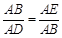 , …………4分
, …………4分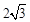 .…………6分
.…………6分 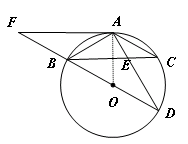
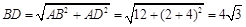 ,
,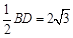 ,…………8分
,…………8分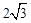 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
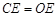 ;③△ODE∽△ADO;④
;③△ODE∽△ADO;④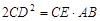 .其中一定正确的结论有( )
.其中一定正确的结论有( )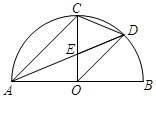
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.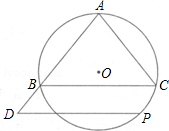
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
. ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com