
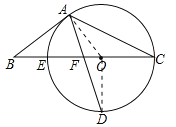
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.

【答案】(1)证明见解析;(2)r=3,sinB=![]() .
.
【解析】
试题分析:(1)连接OA、OD,如图,根据垂径定理得OD⊥BC,则∠D+∠OFD=90°,再由AB=BF,OA=OD得到∠BAF=∠BFA,∠OAD=∠D,加上∠BFA=∠OFD,所以∠OAD+∠BAF=90°,则OA⊥AB,然后根据切线的判定定理即可得到AB是⊙O切线;
(2)先表示出OF=4﹣r,OD=r,在Rt△DOF中利用勾股定理建立方程,解方程得到r的值,那么OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.
然后在Rt△AOB中利用勾股定理,得到AB的值,再根据三角函数定义求出sinB.
试题解析:(1)证明:连接OA、OD,如图,∵点D为CE的下半圆弧的中点,∴OD⊥BC,∴∠EOD=90°,∵AB=BF,OA=OD,∴∠BAF=∠BFA,∠OAD=∠D,而∠BFA=∠OFD,∴∠OAD+∠BAF=∠D+∠BFA=90°,即∠OAB=90°,∴OA⊥AB,∴AB是⊙O切线;
(2)解:OF=CF﹣OC=4﹣r,OD=r,DF=![]() ,在Rt△DOF中,
,在Rt△DOF中,![]() ,即
,即![]() ,解得:r=3或r=1(舍去);∴半径r=3,∴OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.在Rt△AOB中,
,解得:r=3或r=1(舍去);∴半径r=3,∴OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.在Rt△AOB中,![]() ,∴
,∴![]() ,∴AB=4,OB=5,∴sinB=
,∴AB=4,OB=5,∴sinB=![]() =
=![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC![]() △DEF的是( )
△DEF的是( )
A. AB=DE,∠B=∠E,∠C=∠F B. AC=DF,BC=EF,∠C=∠F
C. AB=FE,∠A=∠D,∠B=∠E D. AB=DE,BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有25名同学参加某项比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分
B.中位数
C.方差
D.平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
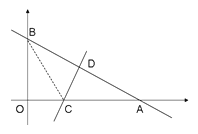
【题目】如图:一次函数y=-![]() x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 。
(2)求OC的长度 ;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com