
某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案由哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?
(成本=材料费+加工费)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
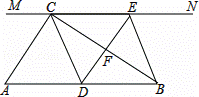
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,在四边形ABCD中,
(1)画出四边形A1B1C1D1,使四边形
A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2.,使四边形
A2B2C2D2与四边形ABCD关于点O中心对称.
(3)四边形A1B1C1D1与四边形A2B2C2D2是否
对称,.若对称请在图中画出对称轴或对称中心.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com