
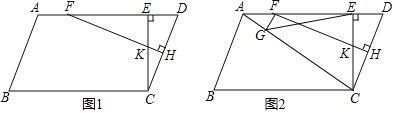
【题目】如图1,在平行四边形ABCD中,过点C作CE⊥AD于点E,过AE上一点F作FH⊥CD于点H,交CE于点K,且KE=DE.
(1)若AB=13,且cosD=![]() ,求线段EF的长;
,求线段EF的长;
(2)如图2,连接AC,过F作FG⊥AC于点G,连接EG,求证:CG+GF=![]() EG.
EG.
【答案】(1)12;(2)详见解析.
【解析】
(1)首先解直角三角形求出EC,再证明△FEK≌△CED(AAS),推出EF=CE=12即可解决问题;
(2)如图,作EM⊥AC于M,EN⊥GF交GF的延长线于N,连接CF.证明△EGN≌△EGM(AAS),推出EN=EM,∵GN=GM,EF=EC,推出Rt△ENF≌Rt△EMC(HL),推出FN=CM,推出CG+GF=GM+CM+GN-FN=2GM=![]() EG;
EG;
(1)解:∵四边形ABCD是平行四边形,
∴AB=CD=13,
∵CE⊥AD,FH⊥CD,
∴∠FHC=∠CED=90°,
在Rt△CDE中,∵cosD=![]() =
=![]() ,
,
∴DE=5,
∴CE=![]() =12,
=12,
∵∠FEK=∠CED=90°,∠FKE=∠CKE,
∴∠EFK=∠ECD,
∵EK=DE,
∴△FEK≌△CED(AAS),
∴EF=CE=12.
(2)证明:如图,作EM⊥AC于M,EN⊥GF交GF的延长线于N,连接CF.
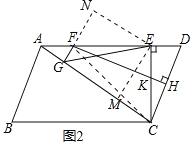
∵FG⊥AC,CE⊥AD,
∴∠FGC=∠FEC=90°,
∵EF=EC,
∴∠EFC=∠ECF=45°,
∴∠FGC+∠FEC=90°,
∴E,F,G,C四点共圆,
∴∠FGE=∠ECF=45°,∠EGC=∠EFC=45°,
∴∠EGN=∠EGM,∵∠EMG=∠ENG=90°,EG=EG,
∴△EGN≌△EGM(AAS),
∴EN=EM,∵GM=GN,EF=EC,
∴Rt△ENF≌Rt△EMC(HL),
∴FN=CM,
∴CG+GF=GM+CM+GN-FN=2GM=![]() EG.
EG.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在对角线BD上,EF∥AB交AD于点F,连接BF.
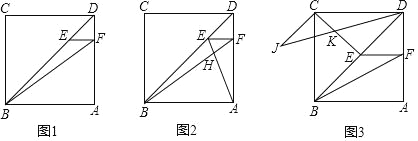
(1)如图1,若AB=4,DE=![]() ,求BF的长;
,求BF的长;
(2)如图2.连接AE,交BF于点H,若DF=HF=2,求线段AB的长;
(3)如图3,连接BF,AB=3![]() ,设EF=x,△BEF的面积为S,请用x的表达式表示S,并求出S的最大值;当S取得最大值时,连接CE,线段DB绕点D顺时针旋转30°得到线段DJ,DJ与CE交于点K,连接CJ,求证:CJ⊥CE.
,设EF=x,△BEF的面积为S,请用x的表达式表示S,并求出S的最大值;当S取得最大值时,连接CE,线段DB绕点D顺时针旋转30°得到线段DJ,DJ与CE交于点K,连接CJ,求证:CJ⊥CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=![]() ,试求m的最大值及此时点P的坐标;
,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
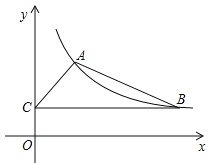
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A,B,C三种货车若干辆,A,B,C每辆货车的日运货量之比为1:2:3,为应对双11物流高峰,该公司重新调配了这三种货车的数量,调配后,B货车数量增加一倍,A,C货车数量各减少50%,三种货车日运货总量增加25%,按调配后的运力,三种货车在本地运完一堆货物需要t天,但A,C两种货车运了若干天后全部被派往外地执行其它任务,剩下的货物由B货车运完,运输总时间比原计划多了4天,且B货车运输时间刚好为A,C两种货车在本地运输时间的6倍,则B货车共运了______天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 函数图象分别位于第一、第三象限
B. 当x>0时,y随x的增大而减小
C. 函数图象经过点(1,2)
D. 若点A(x1,y1),B(x2,y2)都在函数图象上,且x1<x2,则y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了开展阳光体育运动,某市教体局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了600名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).

根据图示,请回答以下问题:
(1)“没时间”的人数是 ,并补全频数分布直方图;
(2)2016年该市中小学生约40万人,按此调查,可以估计2016年全市中小学生每天锻炼超过1h的约有 万人;
(3)在(2)的条件下,如果计划2018年该市中小学生每天锻炼未超过1h的人数降到7.5万人,求2016年至2018年锻炼未超过1h人数的年平均降低的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com