
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

【答案】灯杆AB的长度为2米.
【解析】过点B作BF⊥CE,交CE于点F,过点A作AG⊥AF,交BF于点G,则FG=AC=11.设BF=3x知EF=4x、DF=![]() ,由DE=18求得x=4,据此知BG=BF-GF=1,再求得∠BAG=∠BAC-∠CAG=30°可得AB=2BG=2.
,由DE=18求得x=4,据此知BG=BF-GF=1,再求得∠BAG=∠BAC-∠CAG=30°可得AB=2BG=2.
过点B作BF⊥CE,交CE于点F,过点A作AG⊥AF,交BF于点G,则FG=AC=11.
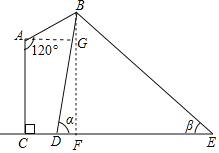
由题意得∠BDE=α,tan∠β=![]() .
.
设BF=3x,则EF=4x
在Rt△BDF中,∵tan∠BDF=![]() ,
,
∴DF=![]() ,
,
∵DE=18,
∴![]() x+4x=18.
x+4x=18.
∴x=4.
∴BF=12,
∴BG=BF-GF=12-11=1,
∵∠BAC=120°,
∴∠BAG=∠BAC-∠CAG=120°-90°=30°.
∴AB=2BG=2,
答:灯杆AB的长度为2米.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证:
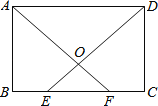
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A. 等边三角形是轴对称图形
B. 若两个图形的对应点连线都被同一条直线垂直平分,则这两个图形关于这条直线对称
C. 若△ABC≌△![]() ,则这两个三角形一定关于一条直线对称
,则这两个三角形一定关于一条直线对称
D. 直线MN是线段AB的垂直平分线,若P点使PA=PB,则点P在MN上,若![]() ,则
,则![]() 不在MN上
不在MN上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板的直角重合放置,如图1所示,
(1)图1中∠BED的度数为 ;
(2)三角板△AOB的位置保持不动,将三角板△COD绕其直角顶点O顺时针方向旋转:
①当旋转至图2所示位置时,恰好OD∥AB,求此时∠AOC的大小;
②若将三角板△COD继续绕O旋转,直至回到图1位置,在这一过程中,是否会存在△COD其中一边能与AB平行?如果存在,请你画出图形,并直接写出相应的∠AOC的大小;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE,CE平分△ABC的两个外角,且交于点E,∠A=80°.
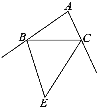
(1)∠E的度数是多少?
(2)若∠ABC=35°,写出四边形ABEC各内角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把 6个相同的小正方体摆成如图的几何体.
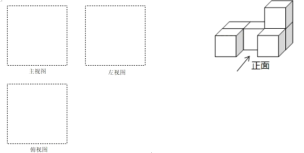
(1)画出该几何体的主视图、左视图、俯视图;
(2)如果每个小正方体棱长为![]() ,则该几何体的表面积是
,则该几何体的表面积是 ![]() .
.
(3)如果在这个几何体上再添加一些相同的小正方体,并并保持左视图和俯视图不变,那么最多可以再 添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的中位数,用max{a,b,c}表示这三个数中最大数,例如:M{﹣2,﹣1,0}=﹣1,max{﹣2,﹣1,0}=0,max{﹣2,﹣1,a}=![]()
解决问题:
(1)填空:M{sin45°,cos60°,tan60°}=__________,如果max{3,5﹣3x,2x﹣6}=3,则x的取值范围为__________;
(2)如果2M{2,x+2,x+4}=max{2,x+2,x+4},求x的值;
(3)如果M{9,x2,3x﹣2}=max{9,x2,3x﹣2},求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C在线段BE上,分别以BC、CE为边作等边三角形ABC和等边三角形DCE,连接AE与CD相交于点N,连接BD与AC相交于点M,连接OC、MN,则以下结论①AE=BD;②△ACN≌△BCM;③∠BOE=120°;④△MNC是等边三角形;⑤OC平分∠BOE;正确的个数是( )
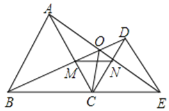
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com