
【题目】如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证:
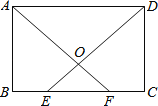
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据矩形的性质可得∠B=∠C=90°,AB=DC,然后求出BF=CE,再利用“边角边”证明△ABF和△DCE全等即可.
(2)根据全等三角形对应角相等可得∠BAF=∠EDC,然后求出∠DAF=∠EDA,然后根据等腰三角形的定义证明即可.
(1)在矩形ABCD中,∠B=∠C=90°,AB=DC,
∵BE=CF,BF=BC﹣FC,CE=BC﹣BE,∴BF=CE.
在△ABF和△DCE中,∵AB=DC,∠B=∠C,BF=CE,
∴△ABF≌△DCE(SAS).
(2)∵△ABF≌△DCE,∴∠BAF=∠EDC.
∵∠DAF=90°﹣∠BAF,∠EDA=90°﹣∠EDC,∴∠DAF=∠EDA.
∴△AOD是等腰三角形.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】城区某新建住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.
(1)若购买树苗共用21000元,问甲、乙两种树苗应各买多少株?
(2)据统计,甲、乙两种树苗每株树苗对空气的净化指数分别为![]() 和
和![]() ,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
查看答案和解析>>
科目:初中数学 来源: 题型:
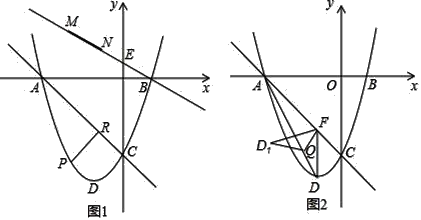
【题目】如图1,已知抛物线y=x2+2x﹣3与x轴相交于A,B两点,与y轴交于点C,D为顶点.
(1)求直线AC的解析式和顶点D的坐标;
(2)已知E(0, ![]() ),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为
),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为![]() 的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
(3)如图2,过点D作DF∥y轴交直线AC于点F,连接AD,Q点是线段AD上一动点,将△DFQ沿直线FQ折叠至△D1FQ,是否存在点Q使得△D1FQ与△AFQ重叠部分的图形是直角三角形?若存在,请求出AQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD沿对角线BD对折,使点C落在![]() 处,连接B
处,连接B![]() 交AD于点E,AB=4, BC=6.
交AD于点E,AB=4, BC=6.
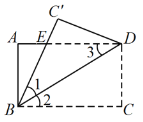
求证: (1)AE=![]() E; (2)△EBD面积.
E; (2)△EBD面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,AB,CB分别交直线m于点D和点E,且DB=DE,若∠1=65°,则∠BDE的度数为( )
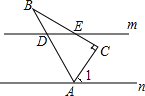
A.115°B.120°C.130°D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
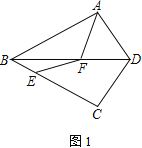
【题目】如图,△ABD、△CBD关于直线BD对称,点E是BC上一点,线段CE的垂直平分线交BD于点F,连接AF、EF.
(1) 求证:AF=EF;
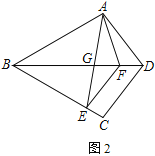
(2) 如图2,连接AE交BD于点G.若EF∥CD,求证:![]() ;
;
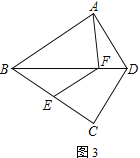
(3) 如图3,若∠BAD=90°,且点E在BF的垂直平分线上,tan∠ABD=![]() ,DF=
,DF=![]() ,请直接写出AF的长.
,请直接写出AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com