
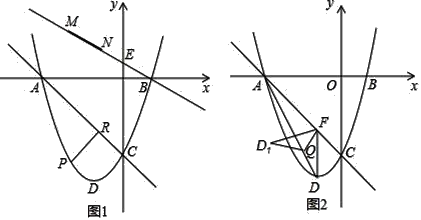
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпy=x2+2xЉ3гыxжсЯрНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌDЮЊЖЅЕуЃЎ
ЃЈ1ЃЉЧѓжБЯпACЕФНтЮіЪНКЭЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉвбжЊEЃЈ0ЃЌ ![]() ЃЉЃЌЕуPЪЧжБЯпACЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌзїPRЁЭACгкЕуRЃЌЕБPRзюДѓЪБЃЌгавЛЬѕГЄЮЊ
ЃЉЃЌЕуPЪЧжБЯпACЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌзїPRЁЭACгкЕуRЃЌЕБPRзюДѓЪБЃЌгавЛЬѕГЄЮЊ![]() ЕФЯпЖЮMNЃЈЕуMдкЕуNЕФзѓВрЃЉдкжБЯпBEЩЯвЦЖЏЃЌЪзЮВЫГДЮСЌНгAЁЂMЁЂNЁЂPЙЙГЩЫФБпаЮAMNPЃЌЧыЧѓГіЫФБпаЮAMNPЕФжмГЄзюаЁЪБЕуNЕФзјБъЃЛ
ЕФЯпЖЮMNЃЈЕуMдкЕуNЕФзѓВрЃЉдкжБЯпBEЩЯвЦЖЏЃЌЪзЮВЫГДЮСЌНгAЁЂMЁЂNЁЂPЙЙГЩЫФБпаЮAMNPЃЌЧыЧѓГіЫФБпаЮAMNPЕФжмГЄзюаЁЪБЕуNЕФзјБъЃЛ
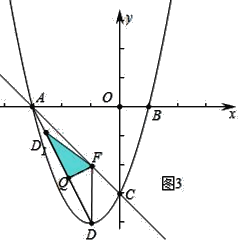
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуDзїDFЁЮyжсНЛжБЯпACгкЕуFЃЌСЌНгADЃЌQЕуЪЧЯпЖЮADЩЯвЛЖЏЕуЃЌНЋЁїDFQбижБЯпFQелЕўжСЁїD1FQЃЌЪЧЗёДцдкЕуQЪЙЕУЁїD1FQгыЁїAFQжиЕўВПЗжЕФЭМаЮЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіAQЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉжБЯпACЕФНтЮіЪНЮЊy=ЉxЉ3ЃЌЕуDзјБъЃЈЉ1ЃЌЉ4ЃЉЃЛЃЈ2ЃЉNЃЈ0ЃЌ ![]() ЃЉЃЛЃЈ3ЃЉAQЕФГЄЮЊ1+
ЃЉЃЛЃЈ3ЃЉAQЕФГЄЮЊ1+![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЗжБ№Сюx=0ЃЌy=0ЃЌПЩЕУAЁЂBЁЂCШ§ЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЩшжБЯпACЕФНтЮіЪНЮЊy=kx+bЃЌзЊЛЏЮЊНтЗНГЬзщМДПЩЃЎ
ЃЈ2ЃЉШчЭМ1жаЃЌЩшPЃЈmЃЌm2+2m-3ЃЉЃЌгЩЬтвтЃЌЕБPRзюДѓЪБЃЌЁїACPЕФУцЛ§зюДѓЃЌМДЫФБпаЮAPCOЕФУцЛ§зюДѓЃЌвђЮЊSЫФБпаЮAPCO=SЁїAOP+SЁїPOC-SЁїAOC=![]() ЁС3ЁСЃЈ-m2-2m+3ЃЉ+
ЁС3ЁСЃЈ-m2-2m+3ЃЉ+![]() ЁС3ЁСЃЈ-mЃЉ-
ЁС3ЁСЃЈ-mЃЉ-![]() ЁС3ЁС3=-
ЁС3ЁС3=-![]() m2-
m2-![]() m=-
m=-![]() ЃЈm+
ЃЈm+![]() ЃЉ2+
ЃЉ2+![]() ЃЌЫљвдЕБm=-
ЃЌЫљвдЕБm=-![]() ЪБЃЌЫФБпаЮAPCOЕФУцЛ§зюДѓЃЌМДPRзюГЄЃЌПЩЕУPЃЈ-
ЪБЃЌЫФБпаЮAPCOЕФУцЛ§зюДѓЃЌМДPRзюГЄЃЌПЩЕУPЃЈ-![]() ЃЌ-
ЃЌ-![]() ЃЉЃЌНЋЕуPбиBEЗНЯђЦНвЦ
ЃЉЃЌНЋЕуPбиBEЗНЯђЦНвЦ![]() ИіЕЅЮЛЕУЕНGЃЈ-
ИіЕЅЮЛЕУЕНGЃЈ-![]() ЃЌ-
ЃЌ-![]() ЃЉЃЌзїЕуAЙигкжБЯпBEЕФЖдГЦЕуKЃЌСЌНгGKНЛBEгкMЃЌДЫЪБЫФБпаЮAPNMЕФзюГЄзюаЁЃЌЯыАьЗЈЧѓГіЕуMЕФзјБъМДПЩНтОіЮЪЬтЃЎ
ЃЉЃЌзїЕуAЙигкжБЯпBEЕФЖдГЦЕуKЃЌСЌНгGKНЛBEгкMЃЌДЫЪБЫФБпаЮAPNMЕФзюГЄзюаЁЃЌЯыАьЗЈЧѓГіЕуMЕФзјБъМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉЗжШ§жжЧщаЮЬжТлМДПЩЂйШчЭМ2жаЃЌЕБFD1ЁЭADЪБЃЌжиЕўВПЗжЪЧRtЁїFKQЃЎЂкШчЭМ3жаЃЌЕБFQЁЭADЪБЃЌжиЕўВПЗжЪЧRtЁїFQD1ЃЌЂлШчЭМ4жаЃЌЕБQD1ЁЭACЪБЃЌжиЕўВПЗжЪЧRtЁїQMFЃЎЗжБ№ЧѓГіAQМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЖдгкХзЮяЯпy=x2+2xЉ3ЃЌСюy=0ЃЌЕУx2+2xЉ3=0ЃЌНтЕУx=Љ3Лђ1ЃЌ
ЁрAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌ
Сюx=0ЃЌЕУy=Љ3ЃЌ
ЁрCЃЈ0ЃЌЉ3ЃЉЃЌ
ЁпХзЮяЯпy=x2+2xЉ3=ЃЈx+1ЃЉ2Љ4ЃЌ
ЁрЖЅЕуDзјБъЮЊЃЈЉ1ЃЌЉ4ЃЉЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊy=kx+bЃЌдђга![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊy=ЉxЉ3ЃЌЕуDзјБъЃЈЉ1ЃЌЉ4ЃЉЃЎ
ЃЈ2ЃЉШчЭМ1жаЃЌЩшPЃЈmЃЌm2+2mЉ3ЃЉЃЌ
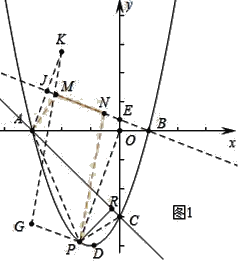
гЩЬтвтЃЌЕБPRзюДѓЪБЃЌЁїACPЕФУцЛ§зюДѓЃЌМДЫФБпаЮAPCOЕФУцЛ§зюДѓЃЌ
ЁпSЫФБпаЮAPCO=SЁїAOP+SЁїPOCЉSЁїAOC=![]() ЁС3ЁСЃЈ-m2-2m+3ЃЉ+
ЁС3ЁСЃЈ-m2-2m+3ЃЉ+![]() ЁС3ЁСЃЈ-mЃЉ-
ЁС3ЁСЃЈ-mЃЉ-![]() ЁС3ЁС3=-
ЁС3ЁС3=-![]() m2-
m2-![]() m=-
m=-![]() ЃЈm+
ЃЈm+![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕБm=Љ![]() ЪБЃЌЫФБпаЮAPCOЕФУцЛ§зюДѓЃЌМДPRзюГЄЃЌ
ЪБЃЌЫФБпаЮAPCOЕФУцЛ§зюДѓЃЌМДPRзюГЄЃЌ
ЁрPЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
НЋЕуPбиBEЗНЯђЦНвЦ![]() ИіЕЅЮЛЕУЕНGЃЈЉ
ИіЕЅЮЛЕУЕНGЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌзїЕуAЙигкжБЯпBEЕФЖдГЦЕуKЃЌСЌНгGKНЛBEгкMЃЌДЫЪБЫФБпаЮAPNMЕФзюГЄзюаЁЃЌ
ЃЉЃЌзїЕуAЙигкжБЯпBEЕФЖдГЦЕуKЃЌСЌНгGKНЛBEгкMЃЌДЫЪБЫФБпаЮAPNMЕФзюГЄзюаЁЃЌ
ЁпжБЯпBEЕФНтЮіЪНЮЊy=Љ![]() x+
x+![]() ЃЌжБЯпAKЕФНтЮіЪНЮЊy=2x+6ЃЌ
ЃЌжБЯпAKЕФНтЮіЪНЮЊy=2x+6ЃЌ
гЩ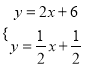 НтЕУ
НтЕУ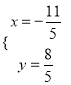 ЃЌ
ЃЌ
ЁрJЃЈЉ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпAJ=JKЃЌ
ЁрkЃЈЉ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁржБЯпKGЕФНтЮіЪНЮЊy=![]() x+
x+![]() ЃЌ
ЃЌ
гЩ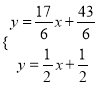 НтЕУ
НтЕУ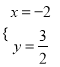 ЃЌ
ЃЌ
ЁрMЃЈЉ2ЃЌ ![]() ЃЉЃЌНЋЕуMЯђЯТЦНвЦ1ИіЕЅЮЛЃЌЯђгвЦНвЦ2ИіЕЅЮЛЕУЕНNЃЌ
ЃЉЃЌНЋЕуMЯђЯТЦНвЦ1ИіЕЅЮЛЃЌЯђгвЦНвЦ2ИіЕЅЮЛЕУЕНNЃЌ
ЁрNЃЈ0ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉДцдкЃЎ
ЂйШчЭМ2жаЃЌЕБFD1ЁЭADЪБЃЌжиЕўВПЗжЪЧRtЁїFKQЃЌзїQMЁЭDFгкMЃЎ
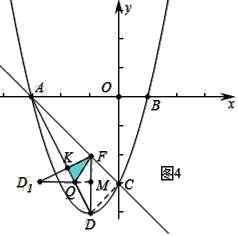
гЩЬтвтПЩжЊFЃЈЉ1ЃЌЉ2ЃЉЃЌDF=2ЃЌAF=2![]() ЃЌAC=3
ЃЌAC=3![]() ЃЌAD=2
ЃЌAD=2![]()
гЩЁїAKFЁзЁїACDЃЌЕУ![]() ЃЌ
ЃЌ
Ёр![]()
ЁрFK=![]() ЃЌAK=
ЃЌAK=![]() ЃЌ
ЃЌ
ЁрDK=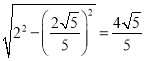 ЃЌЩшQK=QM=xЃЌ
ЃЌЩшQK=QM=xЃЌ
дкRtЁїQMDжаЃЌx2+ЃЈ2Љ![]() ЃЉ2=ЃЈ
ЃЉ2=ЃЈ![]() ЉxЃЉ2ЃЌ
ЉxЃЉ2ЃЌ
Ёрx=1Љ![]() ЃЌ
ЃЌ
ЁрAQ=AK+KQ=1+![]()
ЂкШчЭМ3жаЃЌЕБFQЁЭADЪБЃЌжиЕўВПЗжЪЧRtЁїFQD1ЃЌДЫЪБAQ=![]() ЃЎ
ЃЎ
ЂлШчЭМ4жаЃЌЕБQD1ЁЭACЪБЃЌжиЕўВПЗжЪЧRtЁїQMFЃЎ
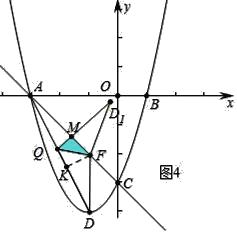
ЩшQM=QK=xЃЌдкRtЁїAQMжаЃЌx2+ЃЈ2![]() Љ
Љ![]() ЃЉ2=ЃЈ
ЃЉ2=ЃЈ![]() ЉxЃЉ2ЃЌ
ЉxЃЉ2ЃЌ
Ёрx=![]()
ЁрAQ=AKЉQK=![]() ЉЃЈ
ЉЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЕБЁїD1FQгыЁїAFQжиЕўВПЗжЕФЭМаЮЪЧжБНЧШ§НЧаЮЪБЃЌAQЕФГЄЮЊ1+![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ
ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌFЪЧCDЩЯвЛЕуЃЌEЪЧBFЩЯвЛЕуЃЌСЌНгAEЁЂACЁЂDEЃЎШєAB=ACЃЌAD=AEЃЌЁЯBAC=ЁЯDAE=70ЁуЃЌAEЦНЗжЁЯBACЃЌдђЯТСаНсТлжаЃКЂйЁїABEЁеЁїACDЃКЂкBE=EFЃЛЂлЁЯBFD=110ЁуЃЛЂмACДЙжБЦНЗжDEЃЌе§ШЗЕФИіЪ§гаЃЈЁЁЁЁЃЉ

A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОеаЦИШЫВХЃЌЖдгІЦИепЗжБ№НјаадФЖСФмСІЁЂзЈвЕжЊЪЖЁЂБэДяФмСІШ§ЯюВтЪдЃЌВЂНЋШ§ЯюВтЪдЕУЗжАД3ЃК5ЃК2ЕФБШР§ШЗЖЈУПШЫЕФзюжеГЩМЈЃЌЯжгћДгМзввСНбЁЪжжаТМШЁвЛШЫЃЌвбжЊСНШЫЕФИїЯюВтЪдЕУЗжШчЯТБэ(ЕЅЮЛЃКЗж)
дФЖС | зЈвЕ | БэДя | |
Мз | 93 | 86 | 73 |
вв | 95 | 81 | 79 |
ЂйЧыЭЈЙ§ЯрЙиЕФМЦЫуЫЕУїЫНЋБЛТМгУЃП
ЂкЧыЖдТфбЁепНёКѓЕФгІЦИЬсаЉКЯРэЕФНЈвщЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋСНИіШЋЕШЕФжБНЧШ§НЧаЮЁїABDЁЂЁїACEЦДдквЛЦ№ЃЈЭМЃЈ1ЃЉЃЉЃЎСюЁїABDВЛЖЏЃЌ
ЃЈ1ЃЉШєНЋЁїACEШЦЕуAФцЪБеыа§зЊЃЌСЌНгDEЃЌMЪЧDEЕФжаЕуЃЌСЌНгMBЁЂMCЃЈЭМЃЈ2ЃЉЃЉЃЌжЄУїЃКMB=MCЃЎ
ЃЈ2ЃЉШєНЋЭМЃЈ1ЃЉжаЕФCEЯђЩЯЦНвЦЃЌЁЯCAEВЛБфЃЌСЌНгDEЃЌMЪЧDEЕФжаЕуЃЌСЌНгMBЁЂMCЃЈЭМЃЈ3ЃЉЃЉЃЌХаЖЯMBЁЂMCЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉжаЃЌШєЁЯCAEЕФДѓаЁИФБфЃЈЭМЃЈ4ЃЉЃЉЃЌЦфЫћЬѕМўВЛБфЃЌдђЃЈ2ЃЉжаЕФMBЁЂMCЕФЪ§СПЙиЯЕЛЙГЩСЂТ№ЃПЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіШ§ЮЛЪ§ЃЌШчЙћАбЫќЕФИіЮЛЪ§зжгыАйЮЛЪ§зжНЛЛЛЮЛжУЃЌФЧУДЫљЕУЕФаТЪ§БШдЪ§аЁ99ЃЌЧвИїЮЛЪ§зжжЎКЭЮЊ14ЃЌЪЎЮЛЪ§зжЪЧИіЮЛЪ§зжгыАйЮЛЪ§зжжЎКЭЃЎЧѓетИіШ§ЮЛЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЕШБпЁїABCжаЃЌвдBCЮЊжБОЖЕФЁбOгыABНЛгкЕуDЃЌDEЁЭACЃЌДЙзуЮЊЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉМЦЫу![]() .
.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЦпФъМЖбЇЩњзМБИШЅЙКТђЁЖгЂККДЪЕфЁЗвЛЪщЃЌДЫЪщБъМлЮЊ20дЊЁЃЯжAЁЂBСНЪщЕъЖМгаДЫЪщГіЪлЃЌAЕъАДШчЯТЗНЗЈДйЯњЃКШєжЛЙКвЛБОЃЌдђАДБъМлЯњЪлЃЛШєвЛДЮадЙКТђЖргквЛБОЃЌЕЋВЛЖрГі20БОЪБЃЌУПЖрЙКвЛБОЃЌУПБОЯњЪлМлдкБъМлЕФЛљДЁЩЯгХЛн2%ЃЈР§ШчТђСНБОЃЌУПБОМлгХЛн2%ЃЛТђШ§БОМлгХЛн4%ЃЌвдДЫРрЭЦЃЉЃЛШєЙКТђЖргк20БОЪБЃЌУПБОЪлМлЮЊ12дЊЃЌBЕъвЛТЩАДБъМлЕФ7елЯњЪлЃЛ
ЃЈ1ЃЉЪдЗжБ№аДГідкСНЪщЕъЙКДЫЪщЕФзмМлyAЁЂyBгыЙКБОЪщЪ§xжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЃЈ2ЃЉШєФГАрвЛДЮадЙКТђЖргк20БОЪБЃЌФЧУДШЅФФМвЪщЕъЙКТђИќКЯЫуЃПЮЊЪВУДЃПШєвЊвЛДЮадЙКТђВЛЖргк20БОЪБЃЌЯШаДГіyЃЈyЃНyAЃyBЃЉгыЙКЪщБОЪ§xжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂдкЭМжаЛГіЦфКЏЪ§ЭМЯѓЃЌдйРћгУКЏЪ§ЭМЯѓЗжЮіШЅФФМвЪщЕъЙКТђИќКЯЫу.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћвЛИіе§ећЪ§ФмБэЪОГЩСНИіСЌајХМЪ§ЕФЦНЗНВюЃЌФЧУДетИіе§ећЪ§ЮЊЁАЩёУиЪ§ЁБ.
ШчЃК![]()
![]()
![]()
вђДЫЃЌ4ЃЌ12ЃЌ20етШ§ИіЪ§ЖМЪЧЩёУиЪ§.
ЃЈ1ЃЉ28КЭ2012етСНИіЪ§ЪЧВЛЪЧЩёУиЪ§ЃПЮЊЪВУДЃП
ЃЈ2ЃЉЩшСНИіСЌајХМЪ§ЮЊ![]() КЭ
КЭ![]() (Цфжа
(Цфжа![]() ЮЊЗЧИКећЪ§)ЃЌгЩетСНИіСЌајХМЪ§ЙЙдьЕФЩёУиЪ§ЪЧ4ЕФБЖЪ§ЃЌЧыЫЕУїРэгЩ.
ЮЊЗЧИКећЪ§)ЃЌгЩетСНИіСЌајХМЪ§ЙЙдьЕФЩёУиЪ§ЪЧ4ЕФБЖЪ§ЃЌЧыЫЕУїРэгЩ.
ЃЈ3ЃЉСНИіСЌајЦцЪ§ЕФЦНЗНВюЃЈШЁе§Ъ§ЃЉЪЧВЛЪЧЩёУиЪ§ЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгавЛПщШ§НЧаЮЭСЕиЃЌЫќЕФЕзБпBC=100УзЃЌИпAH=80УзЃЌФГЕЅЮЛвЊбизХЕиБпBCаовЛзљЕзУцЪЧОиаЮDEFGЕФДѓТЅЃЌDЁЂGЗжБ№дкABЁЂACЕФБпЩЯЃЌЮЪЕБетИіОиаЮУцЛ§зюДѓЪБЃЌЫќЕФГЄгыПэИїЪЧЖрЩйУзЃПУцЛ§зюДѓЮЊЖрЩйЦНЗНУзЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com