
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

【答案】(1)见解析;(2)MB=MC.理由见解析;(3)MB=MC还成立,见解析.
【解析】
(1)连接AM,根据全等三角形的对应边相等可得AD=AE,AB=AC,全等三角形对应角相等可得∠BAD=∠CAE,再根据等腰三角形三线合一的性质得到∠MAD=∠MAE,然后利用“边角边”证明△ABM和△ACM全等,根据全等三角形对应边相等即可得证;
(2)延长DB、AE相交于E′,延长EC交AD于F,根据等腰三角形三线合一的性质得到BD=BE′,然后求出MB∥AE′,再根据两直线平行,内错角相等求出∠MBC=∠CAE,同理求出MC∥AD,根据两直线平行,同位角相等求出∠BCM=∠BAD,然后求出∠MBC=∠BCM,再根据等角对等边即可得证;
(3)延长BM交CE于F,根据两直线平行,内错角相等可得∠MDB=∠MEF,∠MBD=∠MFE,然后利用“角角边”证明△MDB和△MEF全等,根据全等三角形对应边相等可得MB=MF,然后根据直角三角形斜边上的中线等于斜边的一半证明即可.
(1)如图(2),连接AM,由已知得△ABD≌△ACE,
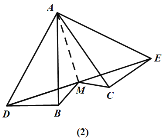
∴AD=AE,AB=AC,∠BAD=∠CAE.
∵MD=ME,
∴∠MAD=∠MAE,
∴∠MAD-∠BAD=∠MAE-∠CAE,
即∠BAM=∠CAM.
在△ABM和△ACM中,
AB=AC,
∠BAM=∠CAM,
AM=AM,
∴△ABM≌△ACM(SAS),
∴MB=MC.
(2)MB=MC.
理由如下:如图(3),延长CM交DB于F,延长BM到G,使得MG=BM,连接CG.
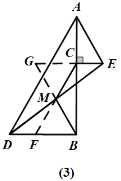
∵CE∥BD,
∴∠MEC=∠MDF,∠MCE=∠MFD.
∵M是ED的中点,
∴MD=ME.
在△MCE和△MFD中,
∠MCE=∠MFD,
∠MEC=∠MDF,
MD=ME,
∴△MCE≌△MFD(AAS).
∴MF=MC.
∴在△MFB和△MCG中,
MF=MC,
∠FMB=∠CMG,
BM=MG,
∴△MFB≌△MCG(SAS).
∴FB=GC,∠MFB=∠MCG,
∴CG∥BD,即G、C、E在同一条直线上.
∴∠GCB=90°.
在△FBC和△GCB中,
FB=GC,
∠FBC=∠GCB,
BC=CB,
∴△FBC≌△GCB(SAS).
∴FC=GB.
∴MB=![]() GB=
GB=![]() FC=MC.
FC=MC.
(3)MB=MC还成立.
如图(4),延长BM交CE于F,延长CM到G,使得MG=CM,连接BG.

∵CE∥BD,
∴∠MDB=∠MEF,∠MBD=∠MFE.
又∵M是DE的中点,
∴MD=ME.
在△MDB和△MEF中,
∠MDB=∠MEF,
∠MBD=∠MFE,
MD=ME,
∴△MDB≌△MEF(AAS),
∴MB=MF.
∵CE∥BD,
∴∠FCM=∠BGM.
在△FCM和△BGM中,
CM=MG,
∠CMF=∠GMB,
MF=MB,
∴△FCM≌△BGM(SAS).
∴CF=BG,∠FCM=∠BGM.
∴CF//BG,即D、B、G在同一条直线上.
在△CFB和△BGC中,
CF=BG,
∠FCB=∠GBC,
CB=BC,
∴△CFB≌△BGC(SAS).
∴BF=CG.
∴MC=![]() CG=
CG=![]() BF=MB.
BF=MB.


科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部工程需![]() 个月,则根据题意可列方程中错误的是( )
个月,则根据题意可列方程中错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() 经过坐标原点,且当
经过坐标原点,且当![]() 时, y随x的增大而减小.
时, y随x的增大而减小.
(1)求抛物线的解析式;
(2)如下图,设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB![]() x轴于点B, DC
x轴于点B, DC![]() x轴于点C.
x轴于点C.
①当 BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a, b),将矩形ABCD的周长L表示为a的函数,并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在平面直角坐标系中的正方形ABCD的边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(如图,它有四个顶点,各顶点数分别是1、2、3、4),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
(1)求点P落在正方形面上(含边界,下同)的概率;
(2)将正方形ABCD平移数个单位,是否存在一种平移,使点P落在正方形面上的概率为![]() ?若存在,指出其中的一种平移方式;若不存在,说明理由.
?若存在,指出其中的一种平移方式;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
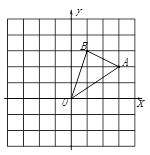
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的的坐标分别为A(3,2)、B(1,3).
⑴.请画出将△AOB向左平移3个单位后得到的图形△A1OB1,点B1的坐标为 ;
⑵.请画出将△AOB关于原点O成对称的图形△A2OB2,点A2的坐标为 ;
⑶.在x轴上找一点P,使PA+PB的值最小,则P点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖用的签字笔可在甲、乙两个商店买到.已知两个商店的标价都是每支签字笔2元.但甲商店的优惠条件是:购买10支以上,从第11支开始按标价的7折卖;乙商店的优惠条件是:从第1支开始就按标价的8.5折卖.
(1)小颖要买20支签字笔,到哪个商店购买较省钱?
(2)小颖现有40元,最多可买多少支签字笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
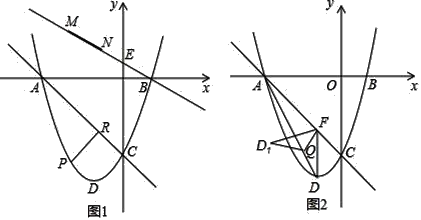
【题目】如图1,已知抛物线y=x2+2x﹣3与x轴相交于A,B两点,与y轴交于点C,D为顶点.
(1)求直线AC的解析式和顶点D的坐标;
(2)已知E(0, ![]() ),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为
),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为![]() 的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
(3)如图2,过点D作DF∥y轴交直线AC于点F,连接AD,Q点是线段AD上一动点,将△DFQ沿直线FQ折叠至△D1FQ,是否存在点Q使得△D1FQ与△AFQ重叠部分的图形是直角三角形?若存在,请求出AQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“英语演讲”比赛活动,八年级(1),(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示,

(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | ______ | 85 | ______ |
八(2) | 85 | ______ | 100 |
(2)计算两班复赛成绩的方差并说明哪版的成绩比较稳定.(方差公式:S2=![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形 ABCD,点 E 在线段 BC 上,连接 DE,点 F 在线段 AB 上,连接 CF、DF, CF 与 DE 交于点 G,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.
(1)求证:CD=CF;
(2)设∠CED= x,∠DCF= y,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当 x=45°时,以 CD 为底边作等腰△CDK,顶角顶点 K 在菱形 ABCD的内部,连接 GK,若 GK∥CD,CD=4 时,求线段 KG 的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com