
【题目】已知:菱形 ABCD,点 E 在线段 BC 上,连接 DE,点 F 在线段 AB 上,连接 CF、DF, CF 与 DE 交于点 G,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.
(1)求证:CD=CF;
(2)设∠CED= x,∠DCF= y,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当 x=45°时,以 CD 为底边作等腰△CDK,顶角顶点 K 在菱形 ABCD的内部,连接 GK,若 GK∥CD,CD=4 时,求线段 KG 的长.


【答案】(1)见解析;(2)y=![]() ;(2)
;(2)![]()
【解析】
(1)根据翻折的性质得△DFG≌△DFA,从而推导得出∠FDC=∠DFG,进而得到CF=DC;
(2)在等腰△DGC和等腰△CFD中,可用y表示出∠GDC、∠FDC的值,从而求出∠ADF,根据∠ADE=∠DEC,得出y与x的关系式;
(3)先证△KCD是等腰直角三角形,根据CD的长得到KC的值,然后再△KGC中求得KG的值.
(1)∵将菱形ABCD沿DF翻折,点A恰好落在点G上
∴△DFG≌△DFA,∠AFD=∠FDC
∴∠AFD=∠DFG
∴∠FDC=∠DFG
∴CF=DC;
(2)∵AD=DG=DC=FC,∠DCF=y
∴在△DGC中,∠DGC=y,∠GDC=180-2y
在△CFD中,∠CFD=∠CDF=![]()
∴∠FDG=∠FDC-∠GDC=![]()
∴∠ADF=∠FDG=![]() ,∴∠ADE=3y-180
,∴∠ADE=3y-180
∵AD∥BC
∴∠ADE=∠DEC,即3y-180=x
化简得:y=![]() ;
;
(3)如下图,过点K作CD的垂线,交CD于点I,延长KG交BC于点L,过点C作GL的垂线,交GL于点Q,过点C作GD的垂线,交GD于点N,
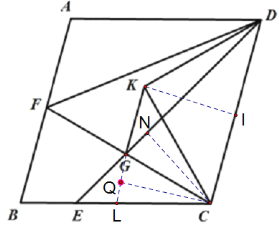
∵x=45°,
∴y=75°,∠ADE=x=45°
∴∠DGC=∠DCG=75°,
∴∠NDC=30°,
∴∠ADC=45°+30°=75°,
∵四边形ABCD是菱形,
∴∠B=75°,
∵KG∥DC,
∴KG∥AB,∠KGD=∠NDC=30°,
∴∠GLC=∠B=75°,∠KGC=30°+75°=105°,
∴∠LGC=75°,
∴∠CGL=∠CGN,
∴GC是∠LGN的角平分线,
∴CQ=CN,
∵CD=4,∠CDE=30°,
∴在Rt△CND中,CN=2,
∴CQ=2,
∵KG∥CD,
∴∠QKI=∠KIC=90°
∵CQ⊥KL
∴四边形CQKI是矩形,
∵CK=KD,KI⊥CD,
∴CI=ID=2,
∴CI=CQ=2,
∴矩形CQKI是正方形
∴IK=CQ=2,
∴在Rt△KIC中,CK=![]() ,
,
如下图,过点G作CK的垂线,交CK于点M,
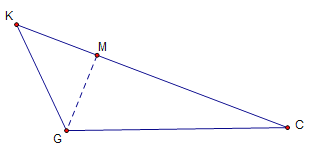
∴△KGM是等腰直角三角形,△GMC是直角三角形,且∠C=30°,
设GM=x,
则在Rt△GKM中,KM=GM=x,
在Rt△GMC中,CG=2x,MC=![]() x,
x,
∴KC=![]() x+x=
x+x=![]() ,
,
解得:x=![]() ,
,
∴KG=![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
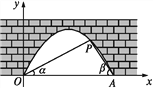
【题目】如图是抛物线型拱桥,P处有一照明灯,水面OA宽4 m,从O,A两处观测P处,仰角分别为α,β,且tan α=![]() ,tan β=
,tan β=![]() ,以O为原点,OA所在直线为x轴建立平面直角坐标系.
,以O为原点,OA所在直线为x轴建立平面直角坐标系.
(1)求点P的坐标.
(2)水面上升1 m,水面宽多少?(结果精确到0.1 m.参考数据: ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数 y=kx+b(k≠0)的图象经过点(-1,-5),(2,1)两点.
(1)求 k 和 b 的值;
(2)一次函数 y=kx+b 图象与坐标轴所围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项![]() ,因式分解的结果是
,因式分解的结果是![]() ,若取
,若取![]() ,
,![]() 时,则各个因式的值是:
时,则各个因式的值是:![]() ,
,![]() ,
,![]() ,于是就可以把“180162”作为一个六位数的密码,对于多项式
,于是就可以把“180162”作为一个六位数的密码,对于多项式![]() ,取
,取![]() ,
,![]() 时,用上述方法产生的密码是________ (写出一个即可).
时,用上述方法产生的密码是________ (写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)

查看答案和解析>>
科目:初中数学 来源: 题型:
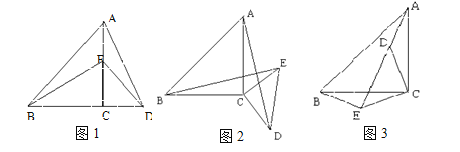
【题目】如图1,E是等腰Rt△ABC边AC上的一个动点(点E与A、C不重合),以CE为一边在Rt△ABC作等腰Rt△CDE,连结AD,BE.我们探究下列图中线段AD,、线段BE 的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的等腰Rt△CDE绕着点C按顺时针方向旋转任意角度![]() ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
(2)将原题中等腰直角三角形改为直角三角形(如图4—6),且AC=a,BC=b,CD=ka,CE=kb (a![]() b,k
b,k![]() 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结BD、AE,且a=4,b=3,k=![]() ,求BD2+AE2的值.
,求BD2+AE2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com