
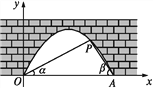
【题目】如图是抛物线型拱桥,P处有一照明灯,水面OA宽4 m,从O,A两处观测P处,仰角分别为α,β,且tan α=![]() ,tan β=
,tan β=![]() ,以O为原点,OA所在直线为x轴建立平面直角坐标系.
,以O为原点,OA所在直线为x轴建立平面直角坐标系.
(1)求点P的坐标.
(2)水面上升1 m,水面宽多少?(结果精确到0.1 m.参考数据: ![]() ≈1.41)
≈1.41)
【答案】(1)点P的坐标为![]() .(2)2.8m.
.(2)2.8m.
【解析】试题分析:(1)过点P作PB⊥OA,垂足为B.设点P的坐标为(x,y).运用三角函数可得![]() 根据条件
根据条件![]() 可求出
可求出![]() ,即可得到点
,即可得到点![]() 的坐标;
的坐标;
(2)若水面上升1m后到达![]() 位置,如图,运用待定系数法可求出抛物线的解析式,然后求出
位置,如图,运用待定系数法可求出抛物线的解析式,然后求出![]() 时
时![]() 的值,就可解决问题.
的值,就可解决问题.
试题解析: (1)如图,过点P作PB⊥OA,垂足为B.设点P的坐标为(x,y).
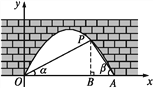
在Rt△POB中,
![]() tan α=
tan α=![]() ,
,
![]() OB=
OB=![]() =2y.
=2y.
在Rt△PAB中,
![]() tan β=
tan β=![]() ,
,
![]() AB=
AB=![]() y.
y.
![]() OA=OB+AB,
OA=OB+AB,
即2y+![]() y=4.
y=4. ![]() y=
y=![]() .
. ![]() x=2×
x=2×![]() =3.
=3.
![]() 点P的坐标为
点P的坐标为![]() .
.
(2)设这条抛物线表示的二次函数为y=ax2+bx.
由函数y=ax2+bx的图象经过(4,0), ![]() 两点,可得
两点,可得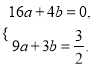
解方程组,得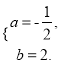
这条抛物线表示的二次函数为y=-![]() x2+2x.
x2+2x.
当水面上升1 m时,水面的纵坐标为1,即-![]() x2+2x=1,
x2+2x=1,
解方程,得x1=2-![]() ,x2=2+
,x2=2+![]() .
.
x2-x1=2+![]() -(2-
-(2-![]() )=2
)=2![]() ≈2.8.
≈2.8.
因此,水面上升1 m,水面宽约为2.8 m.


科目:初中数学 来源: 题型:
【题目】如图,放在平面直角坐标系中的正方形ABCD的边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(如图,它有四个顶点,各顶点数分别是1、2、3、4),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
(1)求点P落在正方形面上(含边界,下同)的概率;
(2)将正方形ABCD平移数个单位,是否存在一种平移,使点P落在正方形面上的概率为![]() ?若存在,指出其中的一种平移方式;若不存在,说明理由.
?若存在,指出其中的一种平移方式;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“英语演讲”比赛活动,八年级(1),(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示,

(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | ______ | 85 | ______ |
八(2) | 85 | ______ | 100 |
(2)计算两班复赛成绩的方差并说明哪版的成绩比较稳定.(方差公式:S2=![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一根 24cm 的筷子,置于底面直径为 15cm,高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 hcm,则 h 的取值范围是( )
A.h≤15cmB.h≥8cmC.8cm≤h≤17cmD.7cm≤h≤16cm
查看答案和解析>>
科目:初中数学 来源: 题型:
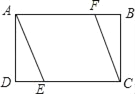
【题目】如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
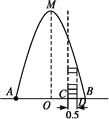
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C处(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4 m,AC=3 m,网球飞行最大高度OM=5 m,圆柱形桶的直径为0.5 m,高为0.3 m(网球的体积和圆柱形桶的厚度忽略不计).
(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形 ABCD,点 E 在线段 BC 上,连接 DE,点 F 在线段 AB 上,连接 CF、DF, CF 与 DE 交于点 G,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.
(1)求证:CD=CF;
(2)设∠CED= x,∠DCF= y,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当 x=45°时,以 CD 为底边作等腰△CDK,顶角顶点 K 在菱形 ABCD的内部,连接 GK,若 GK∥CD,CD=4 时,求线段 KG 的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=![]() ,AD=1.
,AD=1.

(1)求BC的长;
(2)求tan ∠DAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
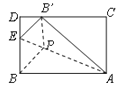
【题目】矩形纸片ABCD中,AB=3,AD=4,将纸片折叠,使点B落在边CD上的B’处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com