
【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
依据SAS可证明ABE≌![]() ,由全等三角形的性质可得到
,由全等三角形的性质可得到![]() ,则
,则![]() ,然后依据四边形的内角和为
,然后依据四边形的内角和为![]() 可求得
可求得![]() 的度数,然后再证明
的度数,然后再证明![]() ,最后,依据等腰三角形的性质可得到AC与DE的关系.
,最后,依据等腰三角形的性质可得到AC与DE的关系.
解:∵AB=AC,∠BAC=∠DAE,AE=AD,
∴ABE≌△ACD,故①正确.
∵ABE≌△ACD,
∴∠AEB=∠ADC.
∵∠AEB+∠AEF=180°,
∴∠AEF+∠ADC=180°,
∴∠BFD=180°-∠EAD=180°-70°=110°,故③正确.
∵AE平分∠BAC,
∴∠EAC=35°.
又∵∠DAE=70°,
∴AC平分∠EAD.
又∵AE=AD,
∴AC⊥EF,AC平分EF.
∴AC是EF的垂直平分线,故④正确.
由已知条件无法证明BE=EF,故②错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADC都是边长相等的等边三角形,点E、F同时分别从点B、A出发,各自沿BA、AD方向运动到点A、D停止,运动的速度相同,连接EC、FC.
(1)在点E、F运动过程中∠ECF的大小是否随之变化?请说明理由;
(2)在点E、F运动过程中,以点A、E、C、F为顶点的四边形的面积变化了吗?请说明理由;
(3)连接EF,在图中找出和∠ACE相等的所有角,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部工程需![]() 个月,则根据题意可列方程中错误的是( )
个月,则根据题意可列方程中错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]()
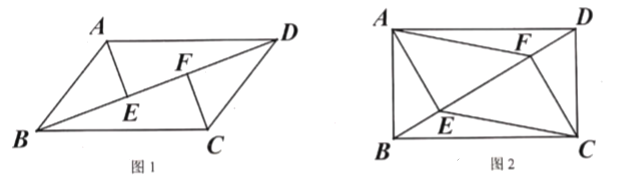
(1)如图1,求证:![]()
(2)如图2,当![]() 时,连接
时,连接![]() 、
、![]() ,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形的面积都等于四边形
,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形的面积都等于四边形![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:把下面的推理过程补充完整,并在括号内注明理由,
如图,已知△ABC中,E、F分别是AB、AC上的两点,且EF∥BC,D为EF上一点,且BD=CD,ED=FD,请说明BE=CF.
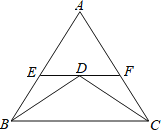
解:∵BD=CD(已知)
∴∠DBC=∠DCB(______)
∵EF∥BC(已知)
∴∠EDB=∠DBC
∠FDC=______(______)
∴∠EDB=∠FDC(等量代换)
在△EBD和△FCD中,
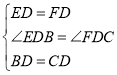
∴△EBD≌△FCD(______)
∴BE=CF(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() 经过坐标原点,且当
经过坐标原点,且当![]() 时, y随x的增大而减小.
时, y随x的增大而减小.
(1)求抛物线的解析式;
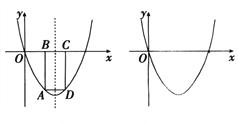
(2)如下图,设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB![]() x轴于点B, DC
x轴于点B, DC![]() x轴于点C.
x轴于点C.
①当 BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a, b),将矩形ABCD的周长L表示为a的函数,并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
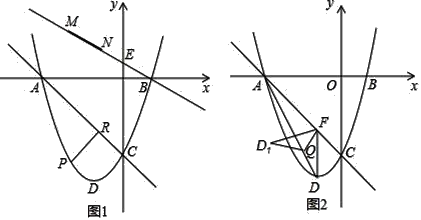
【题目】如图1,已知抛物线y=x2+2x﹣3与x轴相交于A,B两点,与y轴交于点C,D为顶点.
(1)求直线AC的解析式和顶点D的坐标;
(2)已知E(0, ![]() ),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为
),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为![]() 的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
(3)如图2,过点D作DF∥y轴交直线AC于点F,连接AD,Q点是线段AD上一动点,将△DFQ沿直线FQ折叠至△D1FQ,是否存在点Q使得△D1FQ与△AFQ重叠部分的图形是直角三角形?若存在,请求出AQ的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com