
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的中位数,用max{a,b,c}表示这三个数中最大数,例如:M{﹣2,﹣1,0}=﹣1,max{﹣2,﹣1,0}=0,max{﹣2,﹣1,a}=![]()
解决问题:
(1)填空:M{sin45°,cos60°,tan60°}=__________,如果max{3,5﹣3x,2x﹣6}=3,则x的取值范围为__________;
(2)如果2M{2,x+2,x+4}=max{2,x+2,x+4},求x的值;
(3)如果M{9,x2,3x﹣2}=max{9,x2,3x﹣2},求x的值.
【答案】(1)![]() ,
,![]() ;(2)﹣3或0;(3)3或﹣3
;(2)﹣3或0;(3)3或﹣3
【解析】(1)根据定义写出sin45°,cos60°,tan60°的值,确定其中位数;根据max{a,b,c}表示这三个数中最大数,对于max{3,5-3x,2x-6}=3,可得不等式组:则![]() ,可得结论;
,可得结论;
(2)根据新定义和已知分情况讨论:①2最大时,x+4≤2时,②2是中间的数时,x+2≤2≤x+4,③2最小时,x+2≥2,分别解出即可;
(3)不妨设y1=9,y2=x2,y3=3x-2,画出图象,根据M{9,x2,3x-2}=max{9,x2,3x-2},可知:三个函数的中间的值与最大值相等,即有两个函数相交时对应的x的值符合条件,结合图象可得结论.
(1)∵sin45°=![]() ,cos60°=
,cos60°=![]() ,tan60°=
,tan60°= ![]() ,
,
∴M{sin45°,cos60°,tan60°}=![]() ,
,
∵max{3,5-3x,2x-6}=3,
则![]() ,
,
∴x的取值范围为:![]() ≤x≤
≤x≤![]() ;
;
(2)2M{2,x+2,x+4}=max{2,x+2,x+4},
分三种情况:①当x+4≤2时,即x≤-2,
原等式变为:2(x+4)=2,x=-3,
②x+2≤2≤x+4时,即-2≤x≤0,
原等式变为:2×2=x+4,x=0,
③当x+2≥2时,即x≥0,
原等式变为:2(x+2)=x+4,x=0,
综上所述,x的值为-3或0;
(3)不妨设y1=9,y2=x2,y3=3x-2,画出图象,如图所示:
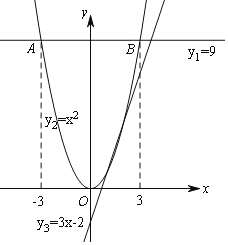
结合图象,不难得出,在图象中的交点A、B点时,满足条件且M{9,x2,3x-2}=max{9,x2,3x-2}=yA=yB,
此时x2=9,解得x=3或-3.


 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
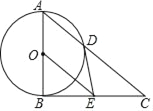
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=![]() ,DE=
,DE=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
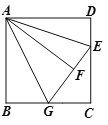
【题目】如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
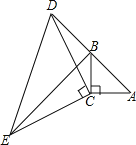
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=2cm,则BE=_______cm.
(3)BE与AD有何位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.

(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com