
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.

(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
【答案】(1)证明见解析(2)4
【解析】
(1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;
(2)作MN⊥AD,根据角平分线的性质得到BM=MN,MN=CM,即![]() .
.
(1)∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,
即AM⊥DM;
(2)过M作MN⊥AD于点N,
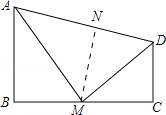
∵AB∥CD,∠B=90°,
∴∠C=90°,即BM⊥AB,MC⊥DC,
又∵AM,DM分别平分∠BAD,∠ADC,BC=8,
∴BM=MN,MN=MC,
∴![]() ,
,
∴M到AD的距离为4.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,点B是数轴上原点O两侧的两点,其中点A在负半轴上,且满足AB=12,OB=2OA.
(1)点A,B在数轴上对应的数分别为 和 ;
(2)点A,B同时分别以每秒2个单位长度和每秒4个单位长度的速度向左运动.
①经过几秒后,OA=3OB;
②点A,B在运动的同时,点P以每秒2个单位长度的速度从原点向右运动,经过几秒后,点A,B,P中的某一点成为其余两点所连线段的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )

A. 14cm B. 17cm C. 20cm D. 23cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() (x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣
(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣ ![]() x+b与抛物线的另一交点为D.
x+b与抛物线的另一交点为D.
(1)若点D的横坐标为﹣5,求抛物线的函数表达式;
(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
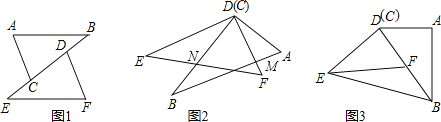
【题目】如图1所示,已知在△ABC和△DEF中,AB=EF,∠B=∠E,EC=BD
(1)试说明:△ABC≌△FED;
(2)若图形经过平移和旋转后得到图2,且有∠EDB=25°,∠A=66°,试求∠AMD的度数;
(3)将图形继续旋转后得到图3,此时D,B,F三点在同一条直线上,若DB=2DF,连接EB,已知△EFB的面积为5cm2,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2105的坐标为_______________.
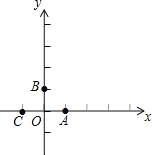
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com