
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=![]() ,DE=
,DE=![]() ,求AD的长.
,求AD的长.
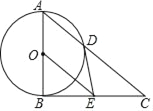
【答案】(1)DE是⊙O的切线,理由见解析;(2)证明见解析;(3)![]()
【解析】(1)先判断出DE=BE=CE,得出∠DBE=∠BDE,进而判断出∠ODE=90°,即可得出结论;
(2)先判断出△BCD∽△ACB,得出BC2=CDAC,再判断出DE=![]() BC,AC=2OE,即可得出结论;
BC,AC=2OE,即可得出结论;
(3)先求出BC,进而求出BD,CD,再借助(2)的结论求出AC,即可得出结论.
(1)DE是⊙O的切线,理由:如图,
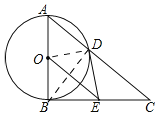
连接OD,BD,∵AB是⊙O的直径,
∴∠ADB=∠BDC=90°,
∵OE∥AC,OA=OB,
∴BE=CE,
∴DE=BE=CE,
∴∠DBE=∠BDE,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODE=∠OBE=90°,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)∵∠BCD=∠ABC=90°,∠C=∠C,
∴△BCD∽△ACB,
∴![]() ,
,
∴BC2=CDAC,
由(1)知DE=BE=CE=![]() BC,
BC,
∴4DE2=CDAC,
由(1)知,OE是△ABC是中位线,
∴AC=2OE,
∴4DE2=CD2OE,
∴2DE2=CDOE;
(3)∵DE=![]() ,
,
∴BC=5,
在Rt△BCD中,tanC=![]() ,
,
设CD=3x,BD=4x,根据勾股定理得,(3x)2+(4x)2=25,
∴x=-1(舍)或x=1,
∴BD=4,CD=3,
由(2)知,BC2=CDAC,
∴AC=![]() ,
,
∴AD=AC-CD=![]() -3=
-3=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )

A. AD=CE B. MF=![]() CF C. ∠BEC=∠CDA D. AM=CM
CF C. ∠BEC=∠CDA D. AM=CM
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把 6个相同的小正方体摆成如图的几何体.
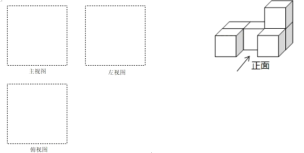
(1)画出该几何体的主视图、左视图、俯视图;
(2)如果每个小正方体棱长为![]() ,则该几何体的表面积是
,则该几何体的表面积是 ![]() .
.
(3)如果在这个几何体上再添加一些相同的小正方体,并并保持左视图和俯视图不变,那么最多可以再 添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).
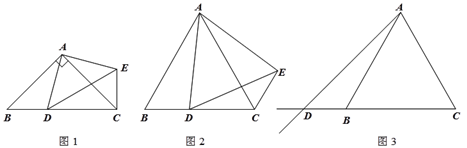
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的中位数,用max{a,b,c}表示这三个数中最大数,例如:M{﹣2,﹣1,0}=﹣1,max{﹣2,﹣1,0}=0,max{﹣2,﹣1,a}=![]()
解决问题:
(1)填空:M{sin45°,cos60°,tan60°}=__________,如果max{3,5﹣3x,2x﹣6}=3,则x的取值范围为__________;
(2)如果2M{2,x+2,x+4}=max{2,x+2,x+4},求x的值;
(3)如果M{9,x2,3x﹣2}=max{9,x2,3x﹣2},求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边上的点F处,折痕为AE.以点A为原点,分别以AD所在的直线为x轴,AB所在的直线为y轴建立坐标系.
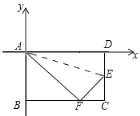
(1)写出点B、D、E、F的坐标;
(2)在坐标轴上是否存在点G,使△AFG是以AF为腰长的等腰三角形?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题.
(1)![]()
(2)![]()
(3)2002-202×198
(4)![]()
(5)[(2x+y)2﹣y(y+4x)﹣8xy]÷(﹣2x).其中x=-2,y=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为:A(-1,2),B(-2,-1),C(2,0).
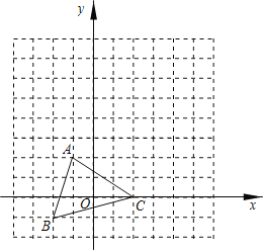
(1)作图:将△ABC先向右平移4个单位,再向上平移3个单位,则得到△A1B1C1,作出△A1B1C1;(不要求写作法)
(2)写出下列点的坐标:A1______;B1______;C1______.
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com