
【题目】如图,BE,CE平分△ABC的两个外角,且交于点E,∠A=80°.
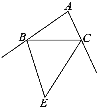
(1)∠E的度数是多少?
(2)若∠ABC=35°,写出四边形ABEC各内角的度数.
【答案】(1)∠E=50°;(2)四边形ABEC各内角的度数为∠A=80°,∠ABE=107.5°,∠E=50°,∠ACE=122.5°.
【解析】
(1)由BE、CE是两外角的平分线,得到![]() 根据三角形的外角的性质和三角形的内角和得到
根据三角形的外角的性质和三角形的内角和得到![]() +∠ABC)=180°,于是得到
+∠ABC)=180°,于是得到![]() 即可得到结论;
即可得到结论;
(2)由∠ABC=35°,根据邻补角的定义得到∠DBC=180°-∠ABC=145°,由BE平分∠DBC,得到![]() ,于是得到
,于是得到![]() ,于是得到
,于是得到![]() ,然后根据四边形的内角和得到结果.
,然后根据四边形的内角和得到结果.
解:(1)如图.∵BE,CE平分△ABC的两个外角,
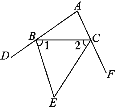
∴∠1=![]() ∠CBD,∠2=
∠CBD,∠2=![]() ∠BCF.
∠BCF.
∵∠CBD=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴∠1=![]() (∠A+∠ACB),∠2=
(∠A+∠ACB),∠2=![]() (∠A+∠ABC).
(∠A+∠ABC).
∵∠E+∠1+∠2=180°,
∴∠E+![]() (∠A+∠ACB)+
(∠A+∠ACB)+![]() (∠A+∠ABC)=180°,
(∠A+∠ABC)=180°,
即∠E+![]() ∠A+
∠A+![]() (∠A+∠ACB+∠ABC)=180°.
(∠A+∠ACB+∠ABC)=180°.
∵∠A+∠ACB+∠ABC=180°,∴∠E+![]() ∠A=90°,
∠A=90°,
∴∠E=90°-![]() ∠A=50°.
∠A=50°.
(2)∵∠ABC=35°,∴∠CBD=180°-∠ABC=145°.
∵BE平分∠CBD,∴∠1=72.5°,
∴∠ABE=35°+72.5°=107.5°,
∴∠ACE=360°-∠A-∠E-∠ABE=122.5°,
∴四边形ABEC各内角的度数为:∠A=80°,
∠ABE=107.5°,∠E=50°,∠ACE=122.5°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,AB,CB分别交直线m于点D和点E,且DB=DE,若∠1=65°,则∠BDE的度数为( )
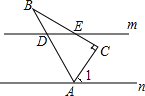
A.115°B.120°C.130°D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O的半径r=2,直线AB不垂直于直线l,过点A,B分别作直线l的垂线,垂足分别为点D,C,则四边形ABCD的面积的最大值为__________.
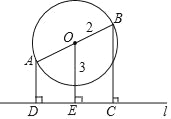
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为______.
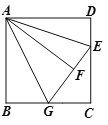
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com