
����Ŀ����a��b��������������ʵ�������ǹ涨�����㲻��ʽa��x��b��ʵ��x������ȡֵ��ȫ����������䣬��ʾΪ[a��b]������һ����������������Ա���x�뺯��ֵy���㣺��m��x��nʱ����m��y��n�����Ǿͳƴ˺����DZ�����[m��n]�ϵġ��պ��������纯��y=��x+4����x=1ʱ��y=3����x=3ʱ��y=1������1��x��3ʱ������1��y��3������˵����y=��x+4�DZ�����[1��3]�ϵġ��պ�������ͬ������y=xҲ�DZ�����[1��3]�ϵġ��պ�������
��1������������y=![]() �DZ�����[1��2018]�ϵġ��պ����������жϲ�˵�����ɣ�
�DZ�����[1��2018]�ϵġ��պ����������жϲ�˵�����ɣ�
��2�������֪���κ���y=x2��4x+k�DZ�����[2��t]�ϵġ��պ���������k��t��ֵ��
��3�������2�������Ķ��κ�����ͼ��y����C�㣬AΪ�˶��κ���ͼ��Ķ��㣬BΪֱ��x=1�ϵ�һ�㣬����ABCΪֱ��������ʱ��д����B�����꣮

���𰸡���1������������y=![]() �DZ�����[1��2018]�ϵġ��պ�������2��t=3��3������ABCΪֱ��������ʱ����B�����꣨1��4+
�DZ�����[1��2018]�ϵġ��պ�������2��t=3��3������ABCΪֱ��������ʱ����B�����꣨1��4+![]() ������1��4��
������1��4��![]() ������1��
������1��![]() ������1��
������1��![]() ��
��
�������������� ��1����k��0��֪����������y=![]() �ڱ�����[1��2016]��y��x���������С��Ȼ��x=1��x=2018����뷴��������ʽ�Ľ���ʽ���Ӷ������y�ķ�Χ�����ǿ������жϣ�
�ڱ�����[1��2016]��y��x���������С��Ȼ��x=1��x=2018����뷴��������ʽ�Ľ���ʽ���Ӷ������y�ķ�Χ�����ǿ������жϣ�
��2������ö��κ����ĶԳ���Ϊx=1��a=1��0�����ݶ��κ��������ʿ�֪y=x2-4x+k�ڱ�����[2��t]��y��x�����������Ȼ��x=2��y=k-4��x=t��y=t2-4t+k�ֱ������κ����Ľ���ʽ���Ӷ������k��ֵ��
��3�����ݹ��ɶ������涨�����ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��⣺
��1����k=2018��
����1��x��2018ʱ��y��x���������С��
����x=1ʱ��y=2018��x=2018ʱ��y=1��
��1��y��2108��
������������y=![]() �DZ�����[1��2018]�ϵġ��պ�������
�DZ�����[1��2018]�ϵġ��պ�������
��2����x=��![]() =2��a=1��0��
=2��a=1��0��
�����κ���y=x2��4x+k�ڱ�����[2��t]��y��x�����������
�����κ���y=x2��2x��k�DZ�����[2��t]�ϵġ��պ�������
����x=2ʱ��y=k��4��x=tʱ��y=t2��4t+k��
![]() ��
��
���k=6��t=3��t=��2��
��Ϊt��2��
��t=2��ȥ��
��t=3��
��3���ɶ��κ�����ͼ��y����C�㣬AΪ�˶��κ���ͼ��Ķ��㣬��
A��2��2����C��0��6����B��1��t����
�ɹ��ɶ�������AC2=22+��2��6��2��AB2=��2��1��2+��2��t��2��BC2=12+��t��6��2��
������ABC=90��ʱ��AB2+BC2=AC2����
��2��1��2+��2��t��2+��t��6��2+1=22+��2��6��2��
����t2��8t+11=0�����t=4+![]() ��t=4��
��t=4��![]() ��
��
B��1��4+![]() ������1��4��
������1��4��![]() ����
����
������BAC=90���ǣ�AB2+AC2=BC2��
����2��1��2+��2��t��2+22+��2��6��2=12+��t��6��2��
����8t=12��
���t=![]() ��
��
B��1��![]() ����
����
������ACB=90��ʱ��AC2+CB2=AB2��
��22+��2��6��2+12+��t��6��2=��2��1��2+��2��t��2��
����2t=13��
���t=![]() ��
��
B��1��![]() ����
����
��������������ABCΪֱ��������ʱ����B�����꣨1��4+![]() ������1��4��
������1��4��![]() ������1��
������1��![]() ������1��
������1��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
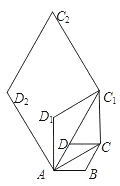
����Ŀ����ͼ���߳�Ϊ![]() ������
������![]() ��
�У�![]() �����ӶԽ���
�����ӶԽ���![]() ����ACΪ�����ڶ�������ACC1D1��ʹ��D1AC��60�㣬����AC1������AC1Ϊ��������������AC1C2D2��ʹ��D2AC1��60�㣻�����˹��������ĵ�2019�����εı߳�Ϊ______.
����ACΪ�����ڶ�������ACC1D1��ʹ��D1AC��60�㣬����AC1������AC1Ϊ��������������AC1C2D2��ʹ��D2AC1��60�㣻�����˹��������ĵ�2019�����εı߳�Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
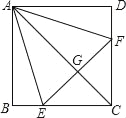
����Ŀ����ͼ��������ABCD�У���E��F�ֱ���BC��CD�ϣ�������AEF�ǵȱ������Σ�����AC��EF��G�����н��ۣ���BE=DF����AG=2GC����BE+DF=EF����S��CEF=2S��ABE��ȷ����_____��ֻ����ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ����һ�㣬
����һ�㣬![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() ����
����![]() ��
��![]()
��1����![]() ��
��![]() ����
����![]() __________��
__________��![]() __________����
__________����![]() ��
��![]() ����
����![]() __________��
__________��![]() __________��
__________��
��2���ɴ˲���![]() ��
��![]() �Ĺ�ϵ����֤��.
�Ĺ�ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
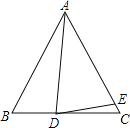
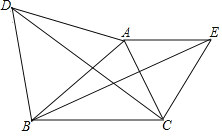
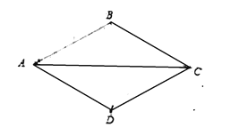
����Ŀ����ͼ����֪��ABC ���ֱ���AB ��AC Ϊ���ڡ�ABC ���ⲿ���ȱ�������ABD�͵ȱ�������ACE����DC ��BE ��˵��DCBE�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������ϵ�ԭ�㿪ʼ���������ƶ�1����λ���ȣ��������ƶ�2����λ���ȣ��������ƶ�3����λ���ȣ��������ƶ�4����λ���ȣ��������ƶ�2019�κõ�����Ӧ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ������
������![]() ��
��![]() ���Խ���
���Խ���![]() �ڵ�
�ڵ�![]() ������
������![]() ��ȡ
��ȡ![]() ���е�
���е�![]() ������
������![]() .
.
��1������������ⲹȫͼ�Σ�
��2����![]() ��������
��������![]() �����Ϊ .��ֱ��д���𰸣�
�����Ϊ .��ֱ��д���𰸣�
��3�����õ�ʽ��ʾ�߶�![]() ��
��![]() ��
��![]() ֮���������ϵ����֤��.
֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ���ϴ�һ�������һ��ֱ�������У��涨�������е�·��Ϊ�������������е�·��Ϊ�������������еĸ���·������Ϊ(��λ������)��-2��-5��+8��-4��+5.
(1)������1����Ϊһ����λ���Ȳ������ϵij�������Ϊԭ�㻭�����ᣬ�������ϱ�ʾ������ÿ�ε����λ��(������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ʾ).
��ʾ).
(2)ֱ��д��������Զ�������������ף�
(3)���������е��ٶȲ��䣬������Щ·�̹���ʱ6���ӣ�ͨ������˵���������е��ٶ��Ƕ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
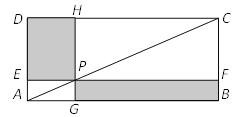
����Ŀ����ͼ��ʾ����P�ھ���ABCD�ĶԽ���AC�ϣ��Ҳ����A��C�غϣ�����P�ֱ�����AB��AD��ƽ���ߣ�������Ա��ڵ�E��F�͵�G��H��
(1)��֤����PHC�ա�CFP��
(2)֤���ı��� PEDH���ı��� PGBF���Ǿ��Σ���ֱ��д���������֮��Ĺ�ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com