
【题目】已知![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() 为
为![]() 上一点,
上一点,![]() ,设
,设![]() ,
,![]()
(1)若![]() ,
,![]() ,则
,则![]() __________;
__________;![]() __________;若
__________;若![]() ,
,![]() ,则
,则![]() __________;
__________;![]() __________;
__________;
(2)由此猜想![]() 与
与![]() 的关系,并证明.
的关系,并证明.
【答案】(1)见解析;(2)![]()
【解析】
(1)先利用等腰三角形的性质求出∠DAE,进而求出∠BAD,即可得出结论;
(2)利用等腰三角形的性质和三角形的内角和即可得出结论.
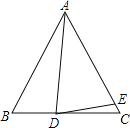
解:(1)①∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°-2∠ADE=40°,
∴α=∠BAD=60°-40°=20°,
∴∠ADC=∠BAD+∠ABD=60°+20°=80°,
∴β=∠CDE=∠ADC-∠ADE=10°,
②同理α=30°;β=15°.
故答案为:20°,10°,30°,15°;
(2)猜想α=2β,理由如下:
设∠ABC=x,∠AED=y,
∴∠ACB=x,∠ADE=y
在△DEC中,y=β+x,
在△ABD中,α+x=y+β=β+x+β,
∴α=2β.


科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
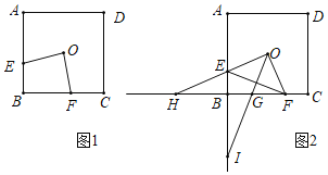
【题目】如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4,则BN的长为__________;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,不写画法,保留作图痕迹,画出一种情形即可)
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 是
是![]() 边上一动点,在
边上一动点,在![]() 上截取
上截取![]() ,连结
,连结![]() ,
,![]() .初步探究:在点
.初步探究:在点![]() 的运动过程中:
的运动过程中:
(1)猜想线段![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
深入探究:
(2)如图2,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .交
.交![]() 的延长线于点
的延长线于点![]() .延长
.延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
①直接写出![]() 的度数.
的度数.
②若![]() ,请探究
,请探究![]() 的值是否为定值,若是,请求出其值;反之,请说明理由
的值是否为定值,若是,请求出其值;反之,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
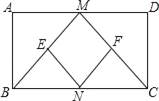
【题目】如图,在矩形ABCD中,M,N分别是AD,BC的中点,E,F分别是线段BM,CM的中点,若AB=8,AD=12,则四边形ENFM的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=![]()

图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS,下面的结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( )
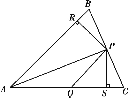
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
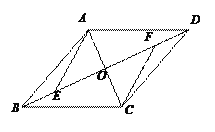
【题目】如图,在□ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连
接AE、CF.
(1)求证△AOE≌△COF;
(2)若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com