
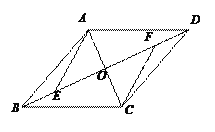
【题目】如图,在□ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连
接AE、CF.
(1)求证△AOE≌△COF;
(2)若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.
科目:初中数学 来源: 题型:
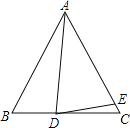
【题目】已知![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() 为
为![]() 上一点,
上一点,![]() ,设
,设![]() ,
,![]()
(1)若![]() ,
,![]() ,则
,则![]() __________;
__________;![]() __________;若
__________;若![]() ,
,![]() ,则
,则![]() __________;
__________;![]() __________;
__________;
(2)由此猜想![]() 与
与![]() 的关系,并证明.
的关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只蚂蚁从一点出发在一条直线上爬行,规定向右爬行的路程为正数,向左爬行的路程为负数,蚂蚁爬行的各段路程依次为(单位:厘米):-2,-5,+8,-4,+5.
(1)请你以1厘米为一个单位长度并将蚂蚁的出发点作为原点画出数轴,在数轴上表示出蚂蚁每次到达的位置(依次用![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示).
表示).
(2)直接写出蚂蚁最远离出发点多少厘米?
(3)若蚂蚁爬行的速度不变,爬完这些路程共用时6分钟,通过计算说明蚂蚁爬行的速度是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
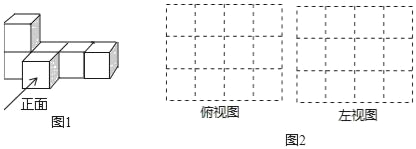
【题目】(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用2B铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需要 个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】预习了“线段、射线、直线”一节的内容后,乐乐所在的小组,对如图展开了激烈的讨论,下列说法不正确的是( )
![]()
A. 直线AB与直线BA是同一条直线
B. 射线OA与射线AB是同一条射线
C. 射线OA与射线OB是同一条射线
D. 线段AB与线段BA是同一条线段
查看答案和解析>>
科目:初中数学 来源: 题型:
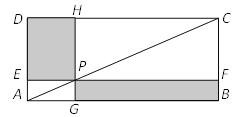
【题目】如图所示,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和点G,H.
(1)求证:△PHC≌△CFP;
(2)证明四边形 PEDH和四边形 PGBF都是矩形,并直接写出它们面积之间的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() >0)的对称轴与x轴交于点B,与直线l:
>0)的对称轴与x轴交于点B,与直线l:![]() 交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
(1) 求抛物线的函数关系式;
(2) 若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按照一定规律排成下表:
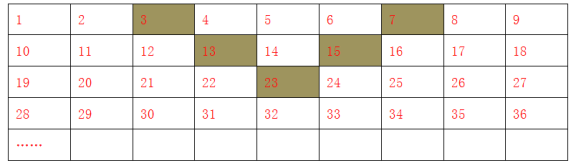
记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a35= ,a54= ;
(2)①若aij=2019,那么i= ,j= ,②用i,j表示aij= ;
(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2026.若能, 求出这5个数中的最小数,若不能请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com