
【题目】已知二次函数![]() >0)的对称轴与x轴交于点B,与直线l:
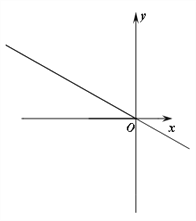
>0)的对称轴与x轴交于点B,与直线l:![]() 交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
(1) 求抛物线的函数关系式;
(2) 若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.
【答案】(1)![]() ;(2) P1(-4,12) ), P2(-4,
;(2) P1(-4,12) ), P2(-4,![]() )
)
【解析】试题分析:(1)把抛物线解析式化为顶点式,可得对称轴为直线 x=-2m,得到C的坐标,由∠DOB=45°,得到BD=BO=2m,即可得到顶点D坐标.过A作AE⊥x轴于E,可求出A的坐标,由△ACD的面积为2,得到m=2,进一步求得顶点D的坐标,从而得到抛物线的解析式;
(2)过P作PM⊥OA于M,则有PM=OM,由直线OA的解析式为:![]() ,设M(n,
,设M(n,![]() ),得到直线PM的解析式,进而得到P的坐标,因为PM=OM,由两点间的距离公式列方程,求出n的值,即可得到P的坐标.
),得到直线PM的解析式,进而得到P的坐标,因为PM=OM,由两点间的距离公式列方程,求出n的值,即可得到P的坐标.
试题解析:解:(1)![]() ,∴对称轴为直线 x=-2m,∴OB=2m,C(-2m,m).∵∠DOB=45°,∴BD=BO=2m,∴则顶点D(-2m,2m).过A作AE⊥x轴于E.∵AC:CO=1:2,∴EB:OB=1:2.∵OB=2m,∴EB=m,∴OE=3m,∴A(-3m,
,∴对称轴为直线 x=-2m,∴OB=2m,C(-2m,m).∵∠DOB=45°,∴BD=BO=2m,∴则顶点D(-2m,2m).过A作AE⊥x轴于E.∵AC:CO=1:2,∴EB:OB=1:2.∵OB=2m,∴EB=m,∴OE=3m,∴A(-3m,![]() ).∵△ACD的面积为2,∴
).∵△ACD的面积为2,∴![]() m·m=2,解得:m=±2 .∵m>0,∴m=2,∴ D(-4,4),∴
m·m=2,解得:m=±2 .∵m>0,∴m=2,∴ D(-4,4),∴![]() ,解得:a=
,解得:a=![]() ,∴
,∴![]() .
.
(2) 如图,过P作PM⊥OA于M.∵∠POC=45°,∴PM=OM.∵直线OA的解析式为:![]() ,设M(n,
,设M(n,![]() ),∴直线PM为
),∴直线PM为![]() ,即:
,即:![]() ,当x=-4时,
,当x=-4时,![]() ,∴P(-4,
,∴P(-4,![]() ).∵PM=OM,∴
).∵PM=OM,∴![]() ,解得:n=-8或n=
,解得:n=-8或n=![]() ,当n=-8时,
,当n=-8时,![]() =12,当n=
=12,当n=![]() 时,
时,![]() =
=![]() ,∴P(-4,12) )或P(-4,
,∴P(-4,12) )或P(-4,![]() ) .
) .



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS,下面的结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( )
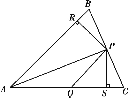
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
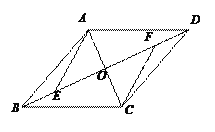
【题目】如图,在□ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连
接AE、CF.
(1)求证△AOE≌△COF;
(2)若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
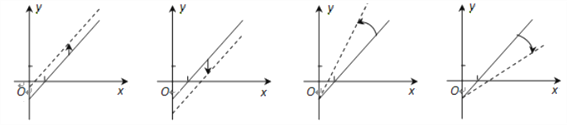
④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(a,0)、B(b,0)(a≠0),a、b满足![]() +b2+2bc+c2=0
+b2+2bc+c2=0
(1) 直接写出a与b的关系
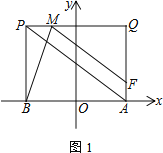
(2) 如图,将线段AB沿y轴的正方向平移m个单位得到线段PQ,点M在线段PQ上,QM=3MP,过M作MF∥PA交QA于点F,连接BM,BM平分∠PMF.若BM=![]() ,求m的值
,求m的值
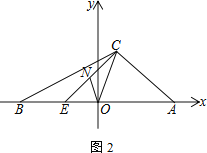
(3) 如图,点C在第一象限内,且满足CA=OA,点E在x轴上,AE=BC,连接CE,取CE的中点N,连接NO.若∠BCA=α,求∠NOC(用含α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
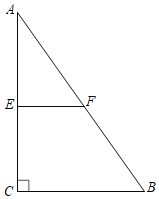
【题目】如图,在直角三角形ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.
(1)求∠A的度数;
(2)求EF和AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④![]() 小时后两人相遇.
小时后两人相遇.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
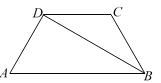
【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
求:(1)求∠CDB的度数;
(2)当AD=2时,求对角线BD的长和梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
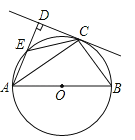
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
(1)求证:CE=CB;
(2)若AC=![]() ,CE=
,CE=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com