
����Ŀ��ij������������·��֧���![]() ��˿���
��˿���![]() �ĺ�����ϵ��ͼ��ʾ����֧���
�ĺ�����ϵ��ͼ��ʾ����֧���![]() ��Ʊ����
��Ʊ����![]() ֧�����ã�������Ŀǰ������·���𣬹�˾�й���Ա������������飺����(��)���ı�֧�����ã���߳�Ʊ�۸���(��)���ı䳵Ʊ�۸���֧������. ����������ĸ�ͼ���У�ʵ�ߺ����߷ֱ��ʾĿǰ�ͽ����ĺ�����ϵ������ ��
֧�����ã�������Ŀǰ������·���𣬹�˾�й���Ա������������飺����(��)���ı�֧�����ã���߳�Ʊ�۸���(��)���ı䳵Ʊ�۸���֧������. ����������ĸ�ͼ���У�ʵ�ߺ����߷ֱ��ʾĿǰ�ͽ����ĺ�����ϵ������ ��
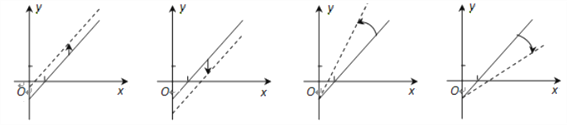
�� �� �� ��
A. �ٷ�ӳ�˽��飨���۷�ӳ�˽��飨�� B. �ڷ�ӳ�˽��飨��)���ܷ�ӳ�˽��飨��
C. �ٷ�ӳ�˽��飨���۷�ӳ�˽��飨�� D. �ڷ�ӳ�˽��飨���ܷ�ӳ�˽��飨��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������ϵ�ԭ�㿪ʼ���������ƶ�1����λ���ȣ��������ƶ�2����λ���ȣ��������ƶ�3����λ���ȣ��������ƶ�4����λ���ȣ��������ƶ�2019�κõ�����Ӧ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC��������������ֱ���A��1��1����B��4��1����C��3��3����
��1������ABC����ƽ��5����λ��õ���A1B1C1���뻭����A1B1C1��
��2������ABC��ԭ��O��ʱ����ת90����õ���A2B2C2���뻭����A2B2C2��
��3���ж���O��A1��BΪ����������ε���״��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԥϰ�ˡ��߶Ρ����ߡ�ֱ�ߡ�һ�ڵ����ݺ��������ڵ�С�飬����ͼչ���˼��ҵ����ۣ�����˵������ȷ����( )
![]()
A. ֱ��AB��ֱ��BA��ͬһ��ֱ��
B. ����OA������AB��ͬһ������
C. ����OA������OB��ͬһ������
D. �߶�AB���߶�BA��ͬһ���߶�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
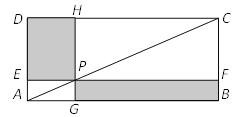
����Ŀ����ͼ��ʾ����P�ھ���ABCD�ĶԽ���AC�ϣ��Ҳ����A��C�غϣ�����P�ֱ�����AB��AD��ƽ���ߣ�������Ա��ڵ�E��F�͵�G��H��
(1)��֤����PHC�ա�CFP��
(2)֤���ı��� PEDH���ı��� PGBF���Ǿ��Σ���ֱ��д���������֮��Ĺ�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
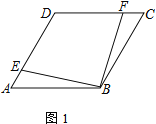
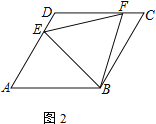
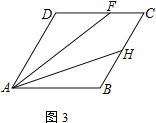
����Ŀ���ı���ABCDΪ���Σ���E�ڱ�AD�ϣ���F�ڱ�CD��
(1) ��AE=CF����֤��EB=BF
(2) ��AD=4��DE=CF������EFBΪ�ȱ������Σ����ı���DEBF�����
(3) ����DAB=60������H�ڱ�BC�ϣ���BH=HC=2������DFA=2��HAB��ֱ��д��CF�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
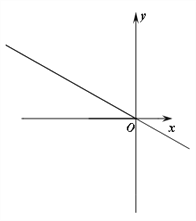
����Ŀ����֪���κ���![]() ��0���ĶԳ�����x�ύ�ڵ�B����ֱ��l��
��0���ĶԳ�����x�ύ�ڵ�B����ֱ��l��![]() ���ڵ�C����A�Ǹö��κ���ͼ����ֱ��l�ڵڶ����Ľ��㣬��D�������ߵĶ��㣬��֪AC��CO��1��2����DOB��45�㣬��ACD�����Ϊ2��
���ڵ�C����A�Ǹö��κ���ͼ����ֱ��l�ڵڶ����Ľ��㣬��D�������ߵĶ��㣬��֪AC��CO��1��2����DOB��45�㣬��ACD�����Ϊ2��
(1) �������ߵĺ�����ϵʽ��
(2) ����PΪ�����߶Գ����ϵ�һ���㣬����POC��45�������P����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����ֽƬABCD��AB=8��AD=6����ֽƬ�۵���ʹ��AD������AB���ϣ��ۺ�ΪAE���ٽ���AED��DE���ҷ��ۣ�AE��BC�Ľ���ΪF����CF�ij�Ϊ________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ͼ����һ����Ϊ![]() ����Ϊ
����Ϊ![]() �ij����Σ���ͼ���������ü������ȷֳ���С�鳤���Σ�Ȼ��ͼ�ҵ���״ƴ��һ��������.
�ij����Σ���ͼ���������ü������ȷֳ���С�鳤���Σ�Ȼ��ͼ�ҵ���״ƴ��һ��������.
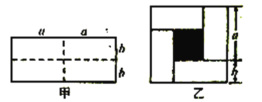
��1����ͼ������Ӱ���������εı߳����ú���ĸ![]() ��
��![]() ����ʽ��ʾ����
����ʽ��ʾ����
��2���������ֲ�ͬ�ķ�����ͼ������Ӱ���ֵ����.
��3���۲�ͼ�ң�����ϣ�2���еĽ��ۣ�д������������ʽ��![]() ��
��![]() ��
��![]() ֮��ĵ�����ϵ��
֮��ĵ�����ϵ��
��4�����ݣ�3�����еĵ�����ϵ������������⣺��![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com